皆さま、こんにちは！

さて、前回は中学入試の最重要テーマのひとつである「相似」について扱いました。

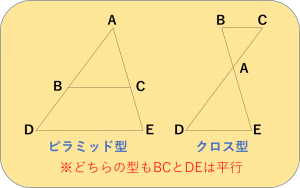
まずは、基本の相似形である「ピラミッド型」と「クロス型」を見つけましょう、ということでした。

 

図を見たときに、このふたつがピンとくるようになりましたでしょうか？

ポイントは、平行線に注目するということでしたね。

平行線は相似形を生む！

この言葉をぜひ覚えておいてください、とお伝えしました。

 

今日は、図形の中にこのふたつを見つけられなかったら？というのがテーマです。

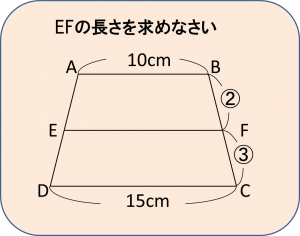
下の問題を見てください。

これは「相似」の利用の典型題で、どんなテキストでも必ず出てくるものです。

受験ドクターの根本原理では、実践編の１１１番に載っていますね。

すでに当たり前に解けるお子さんも多いかと思いますが、試しにやってみてください。

いかがですか？

この問題のポイントは、自分で相似形を作る、ということです。

「相似」の問題の基本は、「ピラミッド型」と「クロス型」を見つけることです。

しかし、いつでも与えられた図の中に、都合よくこの２つがあるわけではありません。

もし、いくら探しても見つからなければ、そのときは自分で作るということを考えましょう。

つまり、補助線を引いて、相似形ができないかを考えるということです。

 

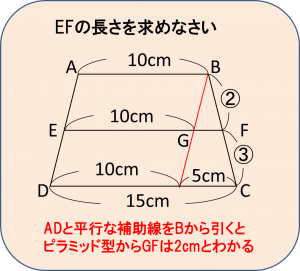
先ほどの問題の最も一般的な補助線の引き方は、以下のように平行線を入れることです。

こうすることで、左側に平行四辺形が、右側にはピラミッド相似ができるので、これで問題は解決します。

詳しい解説は省略しますが、答えは12cmとなりますね。

さて、ここでちょっと考えてみて頂きたいです。

この問題を解くのに他のやり方はないでしょうか？

先ほどの補助線は、一番無駄のない素晴らしい解法なのですが、あえて他の解法も考えてみましょう。

「ピラミッド型」と「クロス型」さえできれば何とかなります。

他にも相似形ができる補助線はないか、少し考えてみてください。

どうですか？

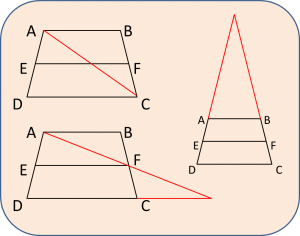
実はこの問題を解くための補助線は、いくつもあります。

以下に例を示しますので、それぞれちゃんと答えが出ることを確かめてみてください。

いかがですか？

どのやり方でもきちんと答えが出るはずです。

ポイントは、どの補助線も「ピラミッド型」と「クロス型」を作るように引いているということです。

この感覚は「相似」の問題を解く際に非常に重要です。

いまのうちにしっかり磨いておきたいですね。

そのためには、ひとつの解法を教わったときに、他のやり方はないのかな？と考えることです。

「相似」の問題は様々な解法がありえることがほとんどなので、積極的に考えてみましょう。

別解を繰り返し考えるうちに、自然と実力がアップしていくはずですよ。

がんばってください！

それでは、また次回お会いしましょう！