みなさん、こんにちは。受験ドクターのAです。

受験ドクターで算、国、理、社の四科目を指導させていただいている幸せな講師です。

 

本日は奥深い約数の話をしたいと思います。

 

もう、年もくれです。

２０１６年も終わり、２０１７年になろうとしています。

 

２０１６年は、2016=２×２×２×２×２×３×３×７

 

という具合に素因数分解できました。

 

では、２０１６の約数の個数は？

 

公式を知っていれば、基本的な問題です。

約数の個数の求め方は、

（素数の数＋１）×（素数の数＋１）×（素数の数＋１）×・・・・・・・＝答え

 

ちなみに、素数とは１とその数以外に約数を持たない整数のことを言います。約数を２つ持つと言った方がいいかもしれません。

 

なぜなら、「１」は約数が１個しかないので素数ではないからです。

 

６年生のこの時期なら１００％知らなければならないので、知らなかったら今すぐ覚えてください。

 

御三家を中心とした難関校を目指しているお子様には、なぜこの公式ができるのかまでを理解させてください。

 

ヒントは「組み合わせ」です。

 

 

さて、だから、２０１６の約数の個数は、２という素数が５個、３という素数が２個、７という素数が１個あるので、赤字の公式に当てはめると、

 

（５＋１）×（２＋１）×（１＋１）＝３６が２０１６の約数の個数になります。

 

ここからが、本日の本題です！２０１７には約数がいくつあるでしょうか！？

 

まずは、基本の確認をしましょう！

 

 

 

２、４、８の倍数は下〇桁が割れるかどうかで判断、３、６、９は各桁を足した数が割れるかどうかで判断するということを忘れないようにしてください。

 

２０１７は奇数なので、２、４、８の倍数でないことが分かります。

 

また各桁を足してみると２＋０＋１＋７＝１０なので３、６、９の倍数でないことが分かります。

 

では、つぎにやることが分かりますか？

 

単純です。「７で割る」です。

 

残念ながら２０１７は７では割れないので７の倍数ではありません。

 

では、つぎにやることが分かりますか？

 

単純です。「11で割る」です。

 

残念ながら２０１７は11では割れないので11の倍数ではありません。

 

では、つぎにやることが分かりますか？

 

「13で割る」です。

 

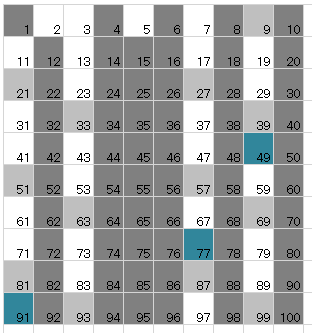
すなわち、どんどん素数で割っていくのです。１～１００までのなかの素数を知っていますか。

 

まずは、先ほども申し上げた通り、１は素数ではありません。

２以外の偶数も２の倍数なので素数ではありません。

 

５以外の５の倍数も消しておきましょう。

 

 

ここからは少し大変です。3以外の３の倍数でまだ消えていないものを消しましょう。

 

 

次は、７以外でまだ消えていない７の倍数を消しましょう。

 

はい、白く残った数字が素数です。

 

もっと簡単に素数を探す方法がないのか？と思われる方もいらっしゃると思いますが、今のところありません。

 

「エラストテネスのふるい」という探し方をご存知の方もいるかもしれませんが、労力はほとんど変わりません。

 

素数の判断方法の公式や、素数の見つけ方の公式を発見したらフィールズ賞（ノーベル賞の数学版だと思ってください）がもらえるかもしれません。

 

では、２０１７が素数かどうかはどんどん素数で割っていくしかないことになります。それでは、どこまで割っていけばいいのか考えていきましょう。

 

２０１７÷１３＝１５５．１・・・割り切れません。

 

２０１７÷１７＝１１８．６・・・割り切れません

 

２０１７÷１９＝１０６．１・・・割り切れません

 

２０１７÷２３＝８７．６・・・割り切れません

 

２０１７÷２９＝６９．５・・・割り切れません

 

２０１７÷３１＝６５．０・・・割り切れません

 

２０１７÷３７＝５４．５・・・割り切れません

 

２０１７÷４１＝４９．１・・・割り切れません

 

２０１７÷４３＝４６．９・・・割り切れません

 

２０１７÷４７＝４２．９・・・割り切れませんが、ここでストップです。

 

なぜ、ここでストップするのかというと、割る数よりも割られた数が大きくなっているからです。

 

割る数よりも割られた数が大きくなっているのに割り切れないということは、今後も割り切れる数は存在しないということなのです。

 

＜まとめ＞

２０１７は素数

 

 

現場で考えるのは辛すぎるので、２０１７は素数だと覚えておく！

 

ちなみに素数には双子素数と呼ばれるものがあります。

それは差が２の２つの素数のことをいいます。

例えば「３と５」、「５と７」、「１１と１３」などです。

 

これは無数にあるのか、それともないのか？

これも未だに証明されていないので、是非、解き明かしてフィールズ賞を獲得してください！

 

では、よいお年をお迎えください。