みなさま、こんにちは。
受験ドクター算数科のHH講師です。

本日は、9月4日（火）ですね。
9月4日が何の日かどうしても気になってしまったので、調べたところ・・・

くしの日でした！！！！（×串ではありません）
9と4でくしの日、非常にわかりやすいですね。

くしと言えば、誰がなんと言っても植木算ですね！！！！

くしは数えるほどしか使ったことがないため知りませんでしたが、とがっている部分を歯と呼ぶそうです。
植木算の考え方を知っていると、くしの歯の数と間の数の関係にすぐに気づきます。
年に一度のくしの日、本日は植木算についておさらいしてみましょう。

植木算は小学4年生に学習する単元ですが、それ以外の単元でもその考え方が必要となるため、重要です。

簡単な例を用いて説明します。
植木算のパターンは3種類です。

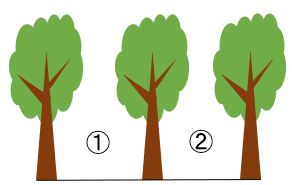
① 両端に木を植える場合
ある道のはしからはしまで等しい間隔で3本の木が植えてあります。
木の本数と間の数の関係について考えてみましょう。

木を3本植えると、間の数は、2か所になります。
木が1本増えて4本になったとすると、間の数は1か所増えて3か所になります。
このように、①のパターンでは、木の数から1を引くと、間の数を求めることができます。

例題
ある道のはしからはしまで、5本の木を10m間隔で植えました。
道の長さは何mですか？

はしからはしまで木を植えるため、パターン①の問題です。
5-1＝4　（間の数）
4×10m＝40m
道の長さは40mとなります。

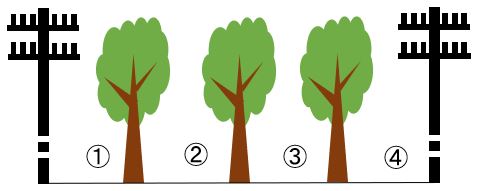
②両端に木を植えない場合
電柱と電柱の間に等しい間隔で木を3本植えます。
木の本数と間の数の関係について考えてみましょう。

木を3本植えると、間の数は、4か所になります。
木が1本増えて4本になったとすると、間の数は1か所増えて5か所になります。
このように、②のパターンでは、木の数に1を足すと、間の数を求めることができます。

例題
電柱と電柱の間に、5m間隔で13本の木を植えることができます。
電柱と電柱の間は何m離れていますか？

はしに電柱があり、木を植えることができませので、パターン②の問題です。
13＋1＝14　（間の数）
14×5m＝70m
電柱と電柱の間の長さは70mとなります。

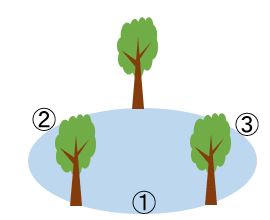
③まわりに木を植える場合
ある池の周りに等しい間隔で木を3本植えます。
木の本数と間の数の関係を考えてみましょう。

木を3本植えると、間の数は、3か所になります。
木が1本増えて4本になったとすると、間の数は1か所増えて4か所になります。
このように、③のパターンでは、木の数と間の数の数が等しくなります。

例題
ある池のまわりに20m間隔で30本の木を植えました。
池のまわりの長さは何mですか？

まわりに木を植えますので、パターン③の問題です。
木の本数と間の数が等しいので、
30×20ｍ＝600m
池のまわりの長さは600mとなります。

このように、植木算は3パターンに分類され、パターンによって木の本数と間の数の関係が異なることを理解しましょう。

では、本題にまいります！！

上にあるくしの長さが何㎝になるのか求めなさい。
ただし、歯の太さは1㎜、間の長さは5㎜、柄の部分は7㎝、歯の数は21本です。
では、挑戦してみましょう！答えは下にあります。

歯の長さ　0.1×21＝2.1㎝
間の長さ　0.5×（21－1）＝10㎝
柄の長さ　7㎝

2.1＋10＋7＝19.1㎝となります。
いかがでしたでしょうか？
木の本数と間の数の関係を思い出し、くしの問題を解くことができましたか？
本日の重要なポイントは、植木算の問題には3パターンあり、それぞれ問題の解き方が異なるところです。
では、また次回お会いしましょう♪