みなさん、こんにちは。受験ドクター算数科のA.K講師です。

今回は、立体図形の単元、その中の回転体について触れていきたいと思います。
平面図形を、ある軸を中心として回したときに出来る立体。イメージがしづらい方もいるのではないでしょうか。
そのアプローチ法について、今年の入試問題をトピックに挙げながらお話ししていきましょう！

【問題】（広尾学園中学校２０１９年度第１回入試大問５より）
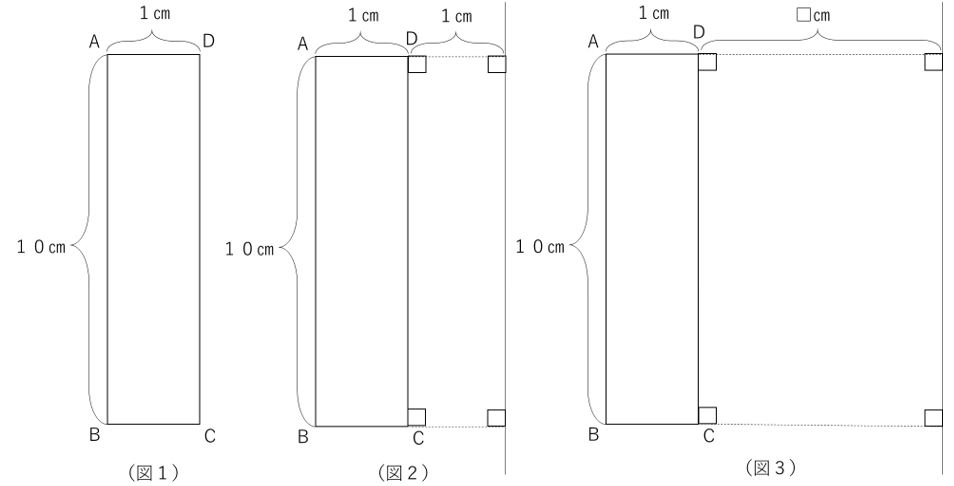
（図１）のような長方形ABCDがあります。次の問いに答えなさい。ただし、円周率は３．１４とします。
（１）（図１）において、辺CDを軸として１回転させてできる立体の体積を求めなさい。
（２）（図２）において、辺CDと平行で、辺CDから１㎝離れた直線を軸として１回転させてできる立体の体積を求めなさい。
（３）（図３）において、辺CDと平行で、辺CDから□㎝離れた直線を軸として１回転させてできる立体の体積を求めたところ、４７１㎤でした。□に入る数を求めなさい。

さて、各々の問題について考えていきますが…その前に！
回転体の考え方について、バシッと１つアドバイス。それは

いきなり全体の図を考えて作図するのではなく、「回る点」について１つ１つ作図をしていく
ということです。
また、「回転」体ですから、底面が三角形や四角形などの角ばった形になることはまず有り得ません。
（１）について考えてみますと、点Aは点Dを中心として１回転するので、半径１㎝の円を描くことになります。

点Bも同様に、点Cを中心として半径１㎝の円を描いて１回転します。
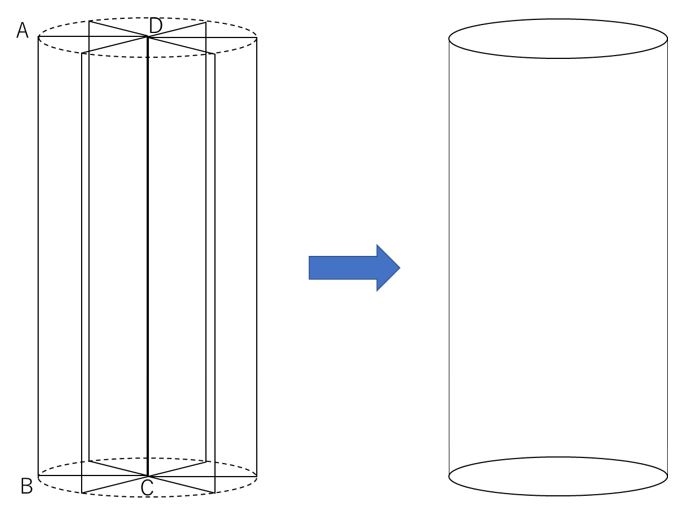
ちょっとずつ回転させてみると、、、

上図のように、底面の円の半径が１㎝、高さが１０㎝の円柱が出来上がるというわけですね！
よって、体積は１×１×３．１４×１０＝３１．４㎤と求まります。
続いて、（２）にいきましょう。
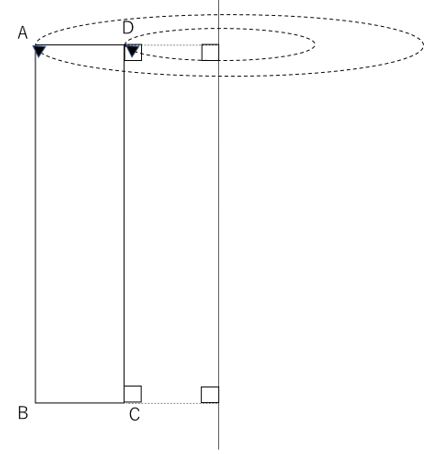
点Dは回転させると半径１㎝の円になり、点Aは回転させると半径２㎝の円になりますね。

点B、点Cも同様に考えると…下のような立体の完成です。

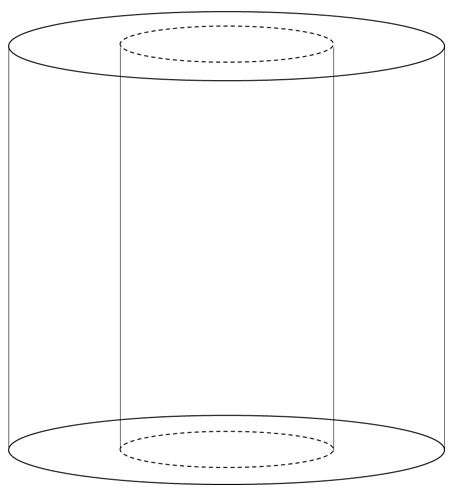
例えるなら、トイレットペーパーのような立体ですね！
底面は半径２㎝の円から半径１㎝の円をくり貫いた形で、高さが１０㎝の円柱が出来上がります。
よって、その体積は（２×２－１×１）×３．１４×１０＝３０×３．１４（←３．１４の工夫は必ずするように！）＝９４．２㎤となります。

（３）については、次回にまたお話ししていきます。それではここで、今日の内容のまとめをしましょう…

～本日のまとめ～
・回転体の問題では、いきなり全体の完成図を思い描くのではなく、段階に分けて１つの点ごとに回転させて出来る図形を作図し、立体の図を完成させる。
・完成した立体の底面の形は円になる。（円から円を取り除いたものもあるが）三角形や四角形などの角がある図形にはならない。

今回はここまで。
次回は、後篇ということで（３）の問題の考え方について触れていこうと思っております。

ではまた、お会いしましょう♪