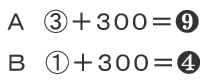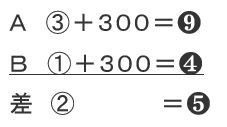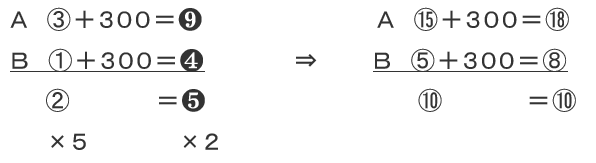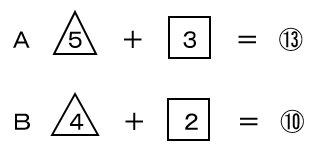みなさん、こんにちは！受験ドクター算数科のA.K講師です。

 

今日が12月29日。今年も早いもので、あと3日で2016年が終わってしまいますね…。

皆様はこの1年間、上手に時間を使うことが出来ましたか？

A.Kは、お子様の指導に一生懸命だったことしか頭にありません^^;

皆様にとって、2017年がより一層充実した年になることを祈っております。

 

では、本題に入りましょう。

前回は、集合算というテーマで表の描き方について主にお伝えしました。

今回は、例題を交えて、割合の観点から比のそろえ方についてお伝えしていきたいと思います。

 

（例題）

Ａ君とＢ君が３：１の割合でお金を持っています。二人とも、お小遣いを３００円ずつもらったので、持っているお金は９：４の割合になりました。最初、Ａ君が持っていたお金はいくらですか？

 

この考え方、倍数算と呼ばれるものです。

10月18日の記事でご紹介したように、大事なことは・・・

 

登場人物を問題文から確認した後、もともと持っていたお金、もらったお金、現在のお金を整理すること！です。

 

実際に式にして整理してみましょう。

 

 

こうなります。次に着目するのは、二人とも同額をもらったので、もともとの差と現在の差が変わらない点です。Ａの式とＢの式の差をとってみましょう。

 

 

以上のようになります。両者の最小公倍数（２と５なので１０）をとり、比を白丸の方に揃えます。白丸の比は５倍、黒丸の比は２倍してＡとＢの式を変化させてみましょう！

 

 

よって、３００円が⑧－⑤＝③となるので、①＝１００円となり、Ａのもともとのお金は⑮＝１００×１５＝１５００円と求まるわけです。

 

 

では、ここからは前回の続きです。

前の記事で、このような入試問題を出題しました。

↓↓↓↓↓↓↓↓↓↓

 

（入試問題　Ｈ２８年度　慶應義塾普通部中学校　大問２）

Ａ地区とＢ地区の小学生の身長について人数を調べました。Ａ地区とＢ地区の小学生全体の人数の比は１３：１０で、１４０ｃｍ以上の人数の比は５：４、１４０ｃｍ未満の人数の比は３：２です。Ａ地区の１４０ｃｍ以上の小学生とＡ地区の１４０ｃｍ未満の小学生の人数の比を求めなさい。

 

 

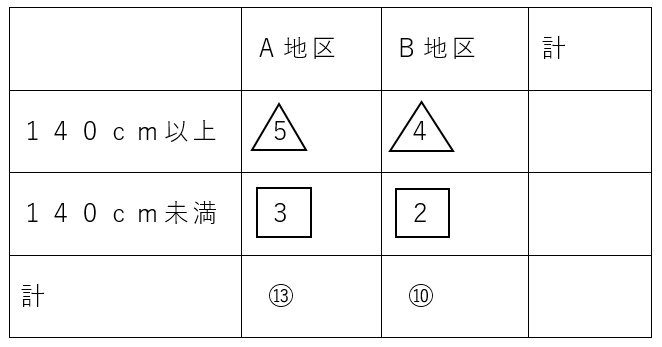
前回は、問題文からグループを整理して下の表にするところまで進みましたよね。

この表から、それぞれの地区について式にしてみます。

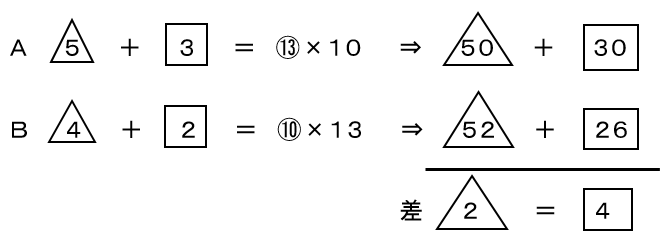
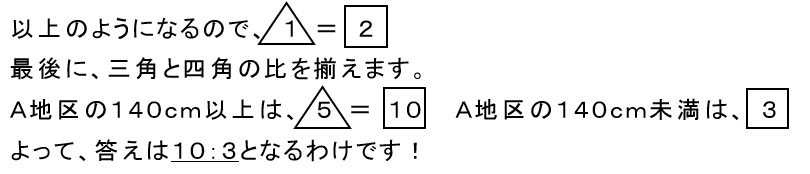
次に、Ａ地区の１４０ｃｍ以上の小学生とＡ地区の１４０ｃｍ未満の小学生の人数の比を問われているので、比を〇の数字の最小公倍数（１３と１０で１３０）に揃えることを考えます。

今回も長々とお付き合いいただき、ありがとうございましたm(_ _)m

というわけで、そろそろ本日のまとめといたしましょう。

 

～今回のポイント～

・倍数算では、登場人物の状態を式にしたあと、それぞれの式を比較し、比をそろえるところは両者の数字の最小公倍数にする

 

ということでした！

 

今日はここまで。

皆様、どうぞよいお年をお迎えください！

また来年、お会いしましょう。