特別編① 2016 第25回算数オリンピックトライアル 問題解説(その1)
はじめに
受験Dr.の亀井章三です。
いつも「開成・筑駒・灘中!すべて合格大作戦!」をお読みいただきありがとうございます。
今回は、いつもの形式を離れた特別編!6月12日(日)に実施された「第25回算数オリンピックトライアル」の問題を1問ずつわかりやすく解説してまいります。
本連載では、いつも応用問題を解くために必要な「解法ポイント」というものをご紹介しています。
今回のトライアル問題を解いていくうえでも、もちろんこの「解法ポイント」を使っていくことで簡単に解いていくことができますので、たくさん「解法ポイント」をご紹介してまいります。
【問題1】
次の式のA、B、C、Dは整数の各けたの数字を表し、すべて0以外のことなる数字です。
ABCD+ABC+BCD+AB+BC+CD+A+B+C+D=2016
このとき、A、B、C、Dそれぞれが表す数字を求めなさい。
第1問は今年の西暦「2016」を題材にした覆面算です。
過去問を解いたことがある方には解きやすかったのではないでしょうか。
このように何ケタかの数字を、記号を使って表した問題には、
【ポイントNo.1】「記号・文字を使って問題文を式に表す」
が使えます。
それでは解説です。
<解説>
2けた以上の数については、次のように表していきます。
ABCD=A×1000+B×100+C×10+D×1
ABC=A×100+B×10+C×1
BCD=B×100+C×10+D×1
AB=A×10+B×1
BC=B×10+C×1
CD=C×10+D×1
これらを問題文の式にあてはめます。
A×1000+B×100+C×10+D×1
+A×100+B×10+C×1
+B×100+C×10+D×1
+A×10+B×1
+B×10+C×1
+C×10+D×1
+A×1+B×1+C×1+D×1
=A×(1000+100+10+1)
+B×(100+10+100+1+10+1)
+C×(10+1+10+1+10+1)
+D×(1+1+1+1)
=A×1111+B×222+C×33+D×4=2016
まずはAから考えます。
A×1111が2016より小さいので、Aは0か1になります。
しかし、Aは一番大きい位の数ですから0はありません。
したがって、A=1です。
Aの分を除いて式を書き替えます。
B×222+C×33+D×4=2016-1111=905
ここで次のポイントを使います。
【ポイントNo.3】「最大値と最小値を考えて範囲を絞る」
C×33+D×4の最小値はC=D=0のときの0
最大値はC=D=9のときの333
よってB×222の値は、572以上905以下となりますので
Bは3か4ということになります。
【ポイントNo.4】「候補が5個以下になったら調べの作業」
のポイントに従い、Bが3のときと4のときに分けて調べます。
B=3のとき
C×33+D×4=905-666=239
これを満たすCとDの組み合わせはC=7、D=2があります。
B=4のとき
C×33+D×4=905-888=17
これを満たすCとDの組み合わせはありません。
したがって、A=1、B=3、C=7、D=2となります。
答え A=1、B=3、C=7、D=2
【問題2】
0~9が書かれたカードを1枚ずつ、横一列にならべました。
すると、どのとなり合う2枚のカードを見てもその差は3か5のどちらかでした。
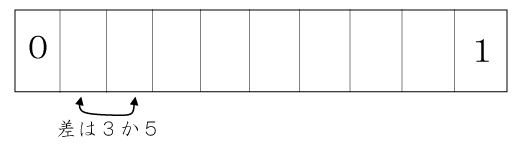
図のように、左端が0、右端が1のとき、残りの8個の数字を正しくならべなさい。
続いての第2問は、数字を条件にしたがって並べる調べ上げの問題です。
ここでは両端から同時に樹形図で進めていく解き方を使っていきます。
<解説>
0と差が3か5の数は3、5。
1と差が3か5の数は4、6です。
これを樹形図にすると、

次に、左から3番目、右から3番目の数を考えます。
3・・・6か8
5・・・2か8
4・・・7か9
6・・・3か9
ここまでを樹形図に書き加えます。
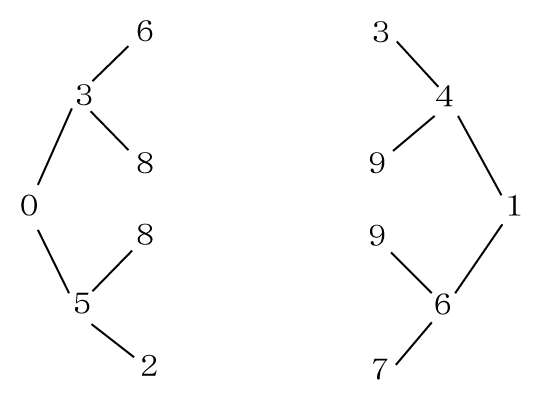
次に、左から4番目、右から4番目の数を考えます。
6・・・1か9
8・・・3か5か9
2・・・7(5はすでに使っているので×)
3・・・6か8
9・・・4か6
7・・・2か4
ここまでを樹形図に書き加えます。
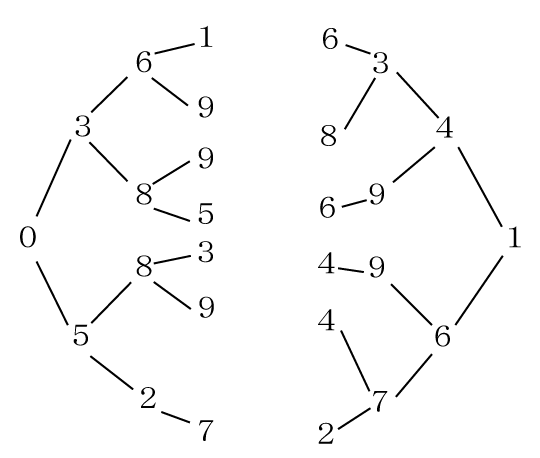
次に、左から5番目だけ考えます。
既に使われている数字によってかなり制限されてきます。
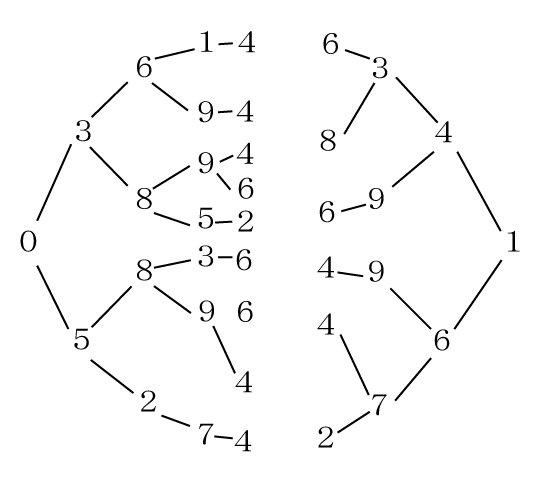
次に、右から5番目だけ考えます。
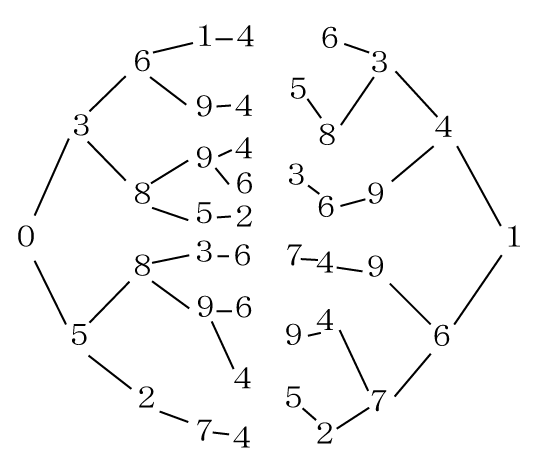
これで10個の数字が出そろいました。
左から5番目にある「2、4、6」と右から5番目にある「3、5、7、9」のうち、
差が3か5なのは「2と5」「2と7」「4と7」「4と9」「6と3」になります。
その組み合わせのみ樹形図でつなぎ、数字が重複しない組み合わせを探すと・・・
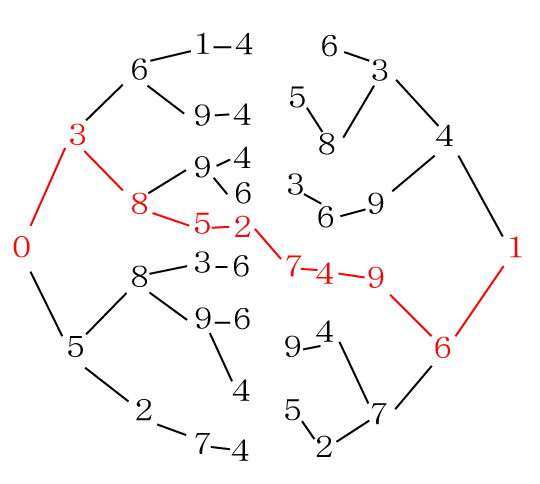
答えは次のようになります。

【問題3】
あるクラスでは、毎日日直と放課後のそうじ当番が一人ずつ割り振られています。
両方の仕事を同じ日にすることはできません。
ある週の月曜日から金曜日は、A君、B君、Cさん、Dさん、E君が日直とそうじ当番の担当でした。
この週のある日の朝の会話を読んで問いに答えなさい。
B君「今週は2日連続で日直とそうじ当番の担当なんだよな。いやだな。」
Dさん「私は今日日直だ…。明後日はそうじ当番なのね。」
E君「今週はもうそうじ当番も終わったし、明日の日直をがんばればいいのか。」
A君「昨日のそうじ中に水そうを割ってしまいました。ごめんなさい。」
Cさん「ねぇ、Dさんは私とそうじ当番の日交換しても日程的に問題ないよね。かわってくれないかな?」
問い:それぞれの曜日の当番がだれであるか答えなさい。
このような会話から推理していく「推理パズル」の問題、まさに算数オリンピックらしい論理的思考が問われる問題です。
普段の受験勉強ではあまり問われないだけに、どれだけ解法を使い慣れているかで差がつくところです。
<解説>
最初に考えなくてはいけないのは、「この会話をしている今日は何曜日なのか?」です。
A君とDさんの会話から、昨日と明後日がある日ということになりますので、今日は火曜日か水曜日となります。
もしも、今日が火曜日だとしたら、A君とE君の会話からこうなります。
E君「もうそうじ当番も終わった」→月曜がそうじ当番
A君「昨日のそうじ中」→月曜がそうじ当番
これは同じ日にそうじ当番が2人いたことになり矛盾しています。したがって、今日は水曜日です。
これにより、次のことがわかります。
・Dさんは「水曜の日直」「金曜のそうじ当番」
・E君は「木曜の日直」「月曜のそうじ当番」
・A君は「火曜のそうじ当番」
次にCさんの会話を見てみましょう。
「Dさんは私とそうじ当番の日交換しても日程的に問題ないよね」
これには2つの意味が隠されています。
1つは、2人ともまだそうじ当番をしていないので、交換しても大丈夫という意味です。
そしてもう1つは、「DさんがCさんとそうじ当番の日を交換しても2人とも日直と同じ日にならない」という意味です。
これにより次のことがわかります。
・Cさんのそうじ当番は「水曜」か「木曜」。
しかし、Dさんは水曜が日直なので、「木曜のそうじ当番」である。
・Cさんは「金曜の日直」ではない。
次に考えるのはB君です。
可能性があるのは、日直が月曜か火曜か金曜。
そうじ当番が水曜日だけです。
したがって、B君は「火曜の日直」「水曜のそうじ当番」と決まります。
日直がまだ決まっていないのはA君とCさん。
曜日は月曜と金曜です。
先ほどのそうじ当番交換のところから、Cさんは金曜の日直ではありませんので、月曜の日直がCさん、金曜の日直がA君と決まり、全て確定しました。
答え 日直 月:C、火:B、水:D、木:E、金:A
そうじ当番 月:E、火:A、水:B、木:C、金:D

