同じことを教えても差がついてしまうのはなぜ？

集団塾で指導していた頃から不思議に思っていたことがあります。
それは同じ熱意をこめた授業をしても、頭のなかに知識がきちんと整理される生徒と、頭のなかが散らかった部屋のようになる生徒に分かれてしまうのは何故か、という疑問です。
生徒たちの学習を観察するうちに、知識を整理できる生徒は、知識を整理できない生徒よりも「自分で気づいた」知識の量がはるかに多いという違いに気づきました。
同じ授業を受けていても、「教わっている子」と「発見する子」では真逆の思考回路が出来上がってゆくのです。

自力で気づいた知識は応用できる

例えば面積図の使い方を指導する場合です。
「問題Aは面積図で解きます」と先生から習っただけの生徒は、問題Aと同じパターンだと認識すれば面積図を使って解けるようになりますが、異なるタイプの問題Bに直面したときにペンが止まってしまいます。
問題Aのときは面積図という回路ができてしまったために、問題Bから面積図を発想することが難しくなります。

「教わり型」

一方で「問題Aが面積図で解ける」ことに自力で気づいた生徒は、問題Bも面積図で解けるのではないかと試行錯誤を行います。仮に問題Bが面積図では解けない問題だったとしても、問題C、問題Dと試行を重ね、面積図はどのようなタイプの問題で使いやすいのかまで体系的に学習を深めることが出来ます。

「発見型」

この２つの学習スタイルの違いが積み重なり、結果的に本来の能力以上に学力に大きな差がついてしまうのです。それが集団授業でのできる子、できない子を分ける線の本質であると考えています。

気づいたきにさせる魔法

算数講師の手腕は、授業の導入部分をみればわかります。
算数の教科書はあくまでも問題とその解法の辞書にすぎません。問題を面白そうと感じさせ、解きたい！といかに思わせるかが講師の最も重要な役割です。
うまい講師は導入の力がずば抜けています。日常とかけ離れた算数の内容をうまく子供達の興味と結びつけ、会話のキャッチボールのなかで解法の鍵となるポイントに気づく手前まで持っていくのです。
この「気づく手前」というのがミソです。
気づく手前まで誘導し、自然に発見を引き起こすことが出来れば、「発見型学習」は成功です。自分で気づいたという感覚が、知識を道具として脳に認識させます。
ここで答えを示してしまうと「教わり型学習」になり、問題ごとに解法を覚えるだけのルーティーンに陥ってしまいます。
つまり、発見型の学習は講師の綿密な導入によって作り出すことが出来るのです。
集団授業のなかで、講師が設定した時間内に気づけなかった生徒たちも、きちんと適切な量のヒントと時間を与えられれば、自ら発見し、知識を組み立てることが出来ます。

だからこそ、私は指導において「5秒待つ感覚」を大切にしています。
もしお子さんが「やっているのに伸びなくなった」「授業についていけてない」と感じていらっしゃるなら、教わり型学習に陥っているでしょう。ヒントの量、タイミング、導入にかける時間が適正でない可能性があります。一人一人に必要な条件をきちんと把握した受験Dr.の講師陣と共に、学習の質から改善してゆきましょう！

一見手がかりがつかめそうにない問題ほどシンプルに捉えることが重要です。
複数の解法を論理的に消去してゆくことで、正解への道筋を絞るトレーニングをマンツーマンで行うことが出来るのは個別指導の醍醐味です。

開成H24年の問題を見てみましょう。

（例題）
AB = 6 cm、BC = 7 cmの三角形ABCの辺BC上に点Dをとり、三角形ABDを2点AとDを通る直線で折り返すと、点Bは右の図1のような点Eに重なります。AEとBCの交わる点をFとすると、CF = 3 cmになり、三角形DEFの面積の7倍になります。
(1) AF、BDのながさをそれぞれ求めなさい。
(2) 三角形ACDを2点AとDを通る直線を軸として回転してできる立体の体積は、三角形ABDを2点AとDを通る直線を軸として回転してできる立体の体積の何倍ですか。ただし、上の図2のような立体を「円すい」といい、その体積は、
（底面の円の面積）×（高さ）÷ 3
で求めることができます。

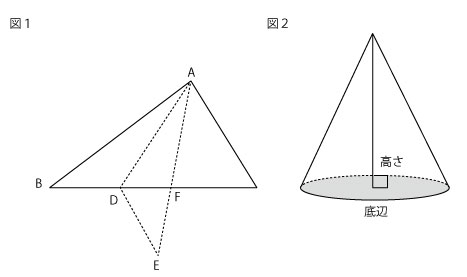
(1)実はこの問題を解くのに必要なポイントは基本中の基本「双子山」の三角形だけなのです。高さが等しい三角形では底辺の比がそのまま面積比となる、という受験生であれば誰もが知っている考え方です。

複雑に見える問題のなかからこのポイントに焦点を絞ってみることで、解法がいもづる式に浮かび上がってきます。

まずは三角形ABCの底辺がBF4cm、CF3cmという条件からシンプルに面積比を置いてみましょう。

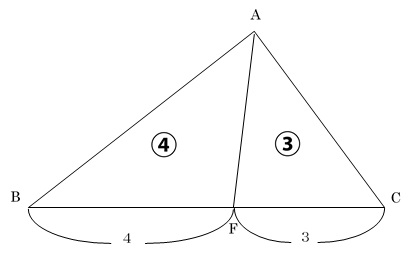
すると三角形ABCは４＋３＝７となり、「ABCの面積がDEFの７倍である」という条件にピタリと当てはまり、三角形DEFは１と表すことができます。
また折り返しであることを考えれば、三角形ABDとAEDは合同ですから、面積はそれぞれ5÷2＝2.5となり、三角形ADFとDEFは1.5：1と表現できます。

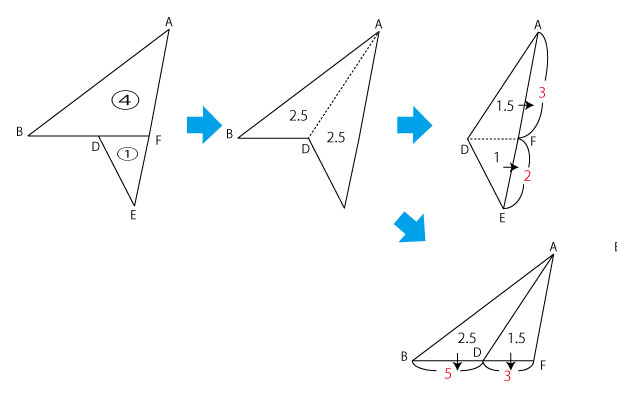
ここで再び「双子山」を使えば、AF：FE＝3：2
AE6ｃｍを比例配分することでAF＝3.6cmと求まります。
同様に三角形ABFに双子山を使うことで、BD：DF＝5：3
比例配分によりBD＝2.5cmとなります。

平面図形が苦手なお子さんは、複雑なものをシンプルにする感覚をつかめていないことが原因のひとつです。すぐに書き込んだり、補助線を入れる発想力は大切ですが、問題をますます難しくしてしまうリスクも伴います。まずは一歩引いた視点で簡単な知識を組み合わせる感覚を養ってゆきましょう。

(2)それぞれの回転体をイメージすると以下の図のようになります。

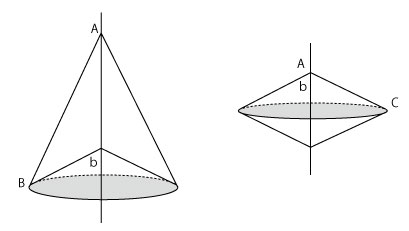
ここでADの長さや底面積が具体的に求まらないことに気づけば、二つの回転体の「共通点と違いに着目し比べる」という発想が得られます。
三角形ABDの回転体は底面積×ADに、三角形ACDの回転体も底面積×ADに変形することが出来ます。

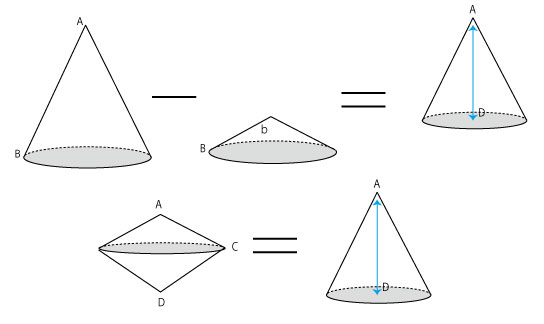
底面積の比がわかれば、すなわち体積の比となりますから
(1)で求めた情報に手がかりを求めましょう。
底面積の半径の比は、三角形ABDとACDの高さの比と同じですから
(1)で書き込んでいた面積比2.5：4.5＝5：9となります。

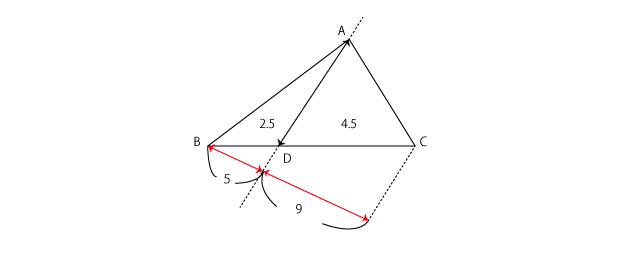
底面積の比は5×5：9×9＝25：81となり倍であることがわかります。

立体図形を底面積×高さの二つの要素にわけて分析することで、複雑な計算は一切なしで解くことができました。このような問題は受験生に、状況を「よりシンプルに」分析し解決する力をこそ求めています。