第18回 複雑な設定の文章題を読み解く
今後の目次
第18回 複雑な設定の文章題を読み解く← 今週はココ!
第19回 正三角形を動かす
第20回 図形の切り分け①~正方形に切る~
今回はまさに「①問題文が長く複雑で、何を言っているのか、何と問われているのかを理解するのが難しい。」という難しさです。長い問題文は一目見ただけでやる気を削がれ、難しい・面倒と感じてしまいます。
しかし、長い問題文を正しく読み取ることができれば、どのように考えていけばよいかのヒントがたくさんあることに気づけます。今回は問題文の読み取りのポイントをご紹介していきます。
ポイントが身につく問題実践講座
問題
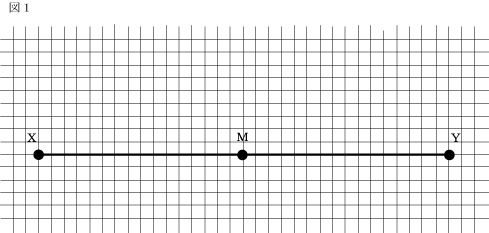
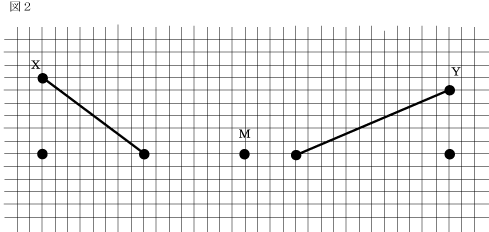
2つの地点X、Yを結ぶ道があります。A君はXからYへ向かって、B君はYからXへ向かって移動し、地図上の中間地点Mで出会うことにしました。地図には等高線が描かれていなかったため、B君は、図1のように2人とも水平な道を移動すると考えました。B君は、自分がA君より速く移動できること、おのおのがつねに同じ速さで移動することの2つをふまえて、A君が出発してから15分後に出発しました。これで、2人はちょうどMで出会うはずでした。 ところが、実際には図2のような下り坂がありました。X%の下り坂では移動する速さがX%だけ増すことになります。ここで下り坂がX%であるとは、
![]()
のことを指します。それでも無事に、2人はちょうどMで出会いました。このとき、以下の問いに答えなさい。なお、3辺の長さの比が3:4:5や5:12:13となる直角三角形を利用してもかまいません。
(1)①A君がXを出発してからMでB君に出会うまでに「実際にかかった時間」は、「事前にB君が想定していた時間」の何倍ですか。
②B君がYを出発してからMでA君に出会うまでに「実際にかかった時間」は、「事前にB君が想定していた時間」の何倍ですか。
(2)A君がXを出発してからMでB君に出会うまでに「実際にかかった時間」を求めなさい。
(2016 開成中 1)
【解くための考え方】
まずは、先ほどの問題を直接お子様に解かせてみてください。
どうでしたか?正解にたどりつけたでしょうか?
正解できなかった場合、どこまで解き進めることができたのかが重要です。
ゲームのルールはわかってもどうすれば勝てるのかがわかりにくいのではないでしょうか。
今後受験Dr.では、「難問攻略イメージde暗記ポイント」カードを作成する予定です。
複雑で長い問題文を正しく読むためには、問題文の構成を考えたり、注意すべき部分に気づいたりすることが大切です。長く複雑な問題文をとらえるためのポイントを1つご紹介します。
今回使うポイント
- 問題文の意味がつかめず条件を整理しにくい
⇒【ポイントNo.35】「聞かれていない数値は適当に設定」
【ポイントNo.35】「聞かれていない数値は適当に設定」
(1)① 文章題が難しく感じられる原因の一つに、割合と比の存在が考えられます。具体的な数字が出てこないために、どうとらえてよいかがわかりにくくなっているのです。
もちろん、そういった点を克服するために、割合と比の使い方に慣れていくことも大切です。しかし、割合をたくさん問題中に使うと今度は処理していくのが大変になってしまいます。
ですから、比を使うべき部分は使い、使わなくてもよい部分は思い切って使わない、という方法を取れると時間短縮と内容の正確な理解の両方達成できるわけです。
そのポイントが「聞かれているかどうか」ということです。
具体的に問題で見ていきましょう。
この問題は速さの問題です。速さには3つの要素があります。それは、時間・距離・速さです。
この3つの要素を「問題文中に具体的な数値で出ているか」「問題として具体的な数値を答えないといけないか」という2つの視点で見てみましょう。
時間・・・問題文中に「15分」と具体的数値が出ている。
設問で「実際にかかった時間」を答えないといけない。
このことから、時間については適当な数値をおくことはできず、比を使って表すことになります。
距離、速さ・・・問題文中に具体的な数字は出てきません。
設問でも問われていません。
このことから、距離と速さについては図の条件に合うのであれば、適当な数値を決めても構わないことになります。
図2は格子状の模様がありますので、これを使って距離を決めます。
X、Y、M以外の地点を下のように表します。
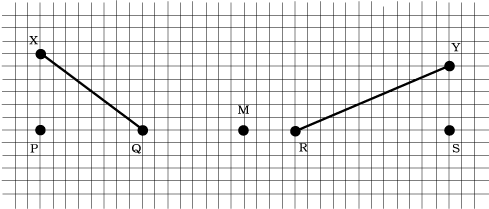
問題文に「なお、3辺の長さの比が3:4:5や5:1213となる直角三角形を利用してもかまいません」とありますが、これは「利用したほうがいいよ~、利用しないとたぶん解けないよ~」と言ってくれているのと同じです。必ず使いましょう。
マス目がありますので、1マス=1㎞と勝手におきます。
すると、QM=8㎞、MR=4㎞になります。
また、XP:PQ=3:4、PQ=8㎞より、XQ=10㎞
YS:SR=5:12、SR=12㎞より、YR=13㎞ です。
次に、A君の速さを毎時8㎞と勝手におきます。これは計算しやすさだけを考えています。
坂道XQの斜度は、
| XP | = | 3 | ×100=75% | ですから、 | |
| PQ | 4 |
A君がXQを下るときの速さは、8×(1+0.75)=毎時14㎞になりますので、A君がXからMまで移動するのにかかる時間は、
| 10÷14+8÷8 | =1 | 5 | 時間となります。 | |
| 7 |
これが、(1)①で出てくる「実際にかかった時間」を勝手に決めた値になります。
では、「事前にB君が想定していた時間」はこの数値を使うといくらになるでしょうか。
図1のXMの距離は16㎞です。ここを毎時8㎞で進みますので、
16÷8=2時間です。
これにより(1)①の答えが求まります。
※解答は(2)の解説の後に見ることができます。
(1)②
B君の実際の動きについて、移動する距離とかかった時間が具体的な数値で与えられたことになりました
| (YR=13㎞、RM=4㎞、合計1 | 5 | 時間)。 |
| 7 |
したがって、B君の速さを勝手におくことができなくなりました。
そこで、B君の速さを毎時3㎞とします。
坂道YRの斜度は、
| YS | = | 5 | ×100= | 125 | % | |
| RS | 12 | 3 |
ですから、
B君がYRを下るときの速さは、
| 3×(1+ | 125 | )=毎時4.25㎞になりますので、 |
| 300 |
B君がYからMまで移動するのにかかる時間は、
| 13÷4.25+4÷3= | 52 | + | 4 | =4 | 20 | 時間となります。 |
| 17 | 3 | 51 |
時間となります。
この値を使って、「事前にB君が想定していた時間」も計算すると
| 16÷3 | = | 16 | 時間、となります。 | |
| 3 |
これにより(1)②の答えが求まります。
※解答は(2)の解説の後に見ることができます。
(2)いよいよ、具体的な数値である「15分」とつなげていきます。
(1)で求めた比を使って考えます。
A君
想定:実際=7:6 想定を⑦分、実際を⑥分とします。
B君
想定:実際=17:14 想定を17分、実際を14分とします。
どちらの場合もB君はA君より15分遅れて出発していますので、
⑥+15=14
⑦+15=17 となります。
よって、⑦-⑥=17-14、①=3となります。
3×6-14=4=15分
A君が実際にかかった時間は⑥分=18分なので、
15÷4×18=67.5分と求まります。
【正解】
| (1)① | 6 | 倍 ② | 14 | 倍 |
| 7 | 17 |
(2)1時間7分30秒
ポイントを使って開成・筑駒・灘の問題を解こう!
問題
A市は、生活用水と農業用水に使用するため、ダムをもっている。このダムの河川からの流入量は例年平均1日1200トンであった。ところが、今年の夏は異常気象のため、河川からの流入量は年間平均の60%になるだろうと気象台から通報を受けた。そこでダムの貯水量が満水時の80%になったときに、A市は対策会議を開いたところ、現在の生活用水毎日Xトン、農業用水毎日400トンの給水を続けると、90日間でダムは空になるという結論が出た。
ところが河川からの流入量が年間平均の40%にとどまったため、30日後にはダムの貯水量は満水時の50%になってしまった。
(1)Xはいくらですか。
(2)ダムの満水量は何トンですか。
A市は緊急対策として、農業用水は1日350トンに減らし、生活用水も減らして、ダムが空になるまで今後60日間給水を続けることにした。
(3)生活用水を減らす割合は何%ですか。答えは小数第2位以下を切り上げて、小数第1位までで求めなさい。
(1995 灘中(二日目)3)
【解説】
(1)(2)
この問題もいろいろ条件が出てきて、うまく整理していかないと何をしていいかがわかりません。どのような数値があるのでしょうか。
増える量、減る量、はじめの量の3つが出てきます。
それぞれについて、具体的な数値が出ているか・問題で具体的な数値が聞かれているかを考えていきます。
増える量=河川からの流入量
→「平均1日1200トン」と具体的な数値あり
減る量=農業用水・生活用水
→「400トン」「350トン」と具体的数値あり。また(1)でも具体的な数値を答える必要あり
はじめの量=満水時のダムの貯水量
→(2)で具体的な数値を答える必要あり
したがって、今回は適当な数値をあてはめるのではなく、割合を記号化(○や□で囲んだもの)して式を作っていきます。←ポイント№35
問題文で具体的な数値が出てきていない「満水時のダムの貯水量」を、
100とします。ここで100としたのは、他の貯水量が%で表されているので計算しやすくするためです。
では、問題文の状況を1つずつ整理します。
①最初の予定
80トンの水がダムにあります。
1日あたり1200×0.6=720トンの水が入ってきます。
一方、1日あたり(X+400)トンの水が出ていきます。
この80トンの水が90日で空になるので、
{(X+400)-720}×90=80
(X-320)×90=80
となります。
②実際の変化(緊急対策前)
最初ダムにあった水の量と、1日あたり出ていく水の量は①と同じ。
1日あたり1200×0.4=480トンの水が入ってきます。
80トンの水が30日で50トンになるので、
{(X+400)-480}×30=80-50
(X-80)×30=30
①、②の2つの式を並べます。
(X-320)×90=80 →X×90-28800=80
(X-80)×30=30 →X×30-2400=30 →X×90-7200=90
よって、28800+80=7200+90 → 28800-7200=90-80
→ 21600=10
したがって、満水時のダムの貯水量100=21600×10=216000トンが求まります。
また、(X-80)×30=21600×3 → X=2240 も求まります。
答え (1)X=2240 (2)216000トン
(3)
緊急対策で減らした生活用水の水量を1日あたりYトンとします。
③緊急対策
この時点のダムの水量は216000×0.5=108000トン
1日あたり1200×0.4=480トンの水が入ってきます。
一方、1日あたり(Y+350)トンの水が出ていきます。
この108000トンの水が60日で空になるので、
{(Y+350)-480}×60=108000
(Y-130)×60=108000 となります。
よって、Y-130=108000÷60=1800
Y=1800+130=1930 となります。
最初の2240トンから、2240-1930=310トン減らしています。
この割合が答えになります。
310÷2240=0.13839…=13.839…%
小数第2位で切り上げなので、答えは13.9%になります。
答え 13.9%
ポイントが確認できるチャレンジ問題 前回の答え
問題
下の展開図を組み立ててできる立体の体積は何㎠ですか。
ただし三角形の面はどれも正三角形で、六角形の面はどれも1辺が2㎝の正方形から等しい2辺の長さが1㎝の直角二等辺三角形2つを切り取ってできる図形である。
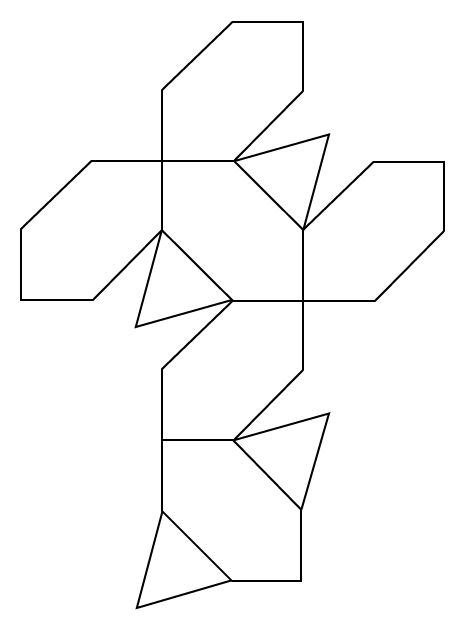
(2005 灘中(1日目)13)
【解説】
問題文にある、「六角形の面はどれも1辺が2㎝の正方形から等しい2辺の長さが1㎝の直角二等辺三角形2つを切り取ってできる図形」という部分に注目しましょう。
この立体のもともとの形には、1辺が2㎝の正方形の面が6面あったことがわかります。つまり、この立体は立方体から四隅を切り取った立体になります。
切り口の形が正三角形になることをふまえて、立体を再現すると下のようになります。
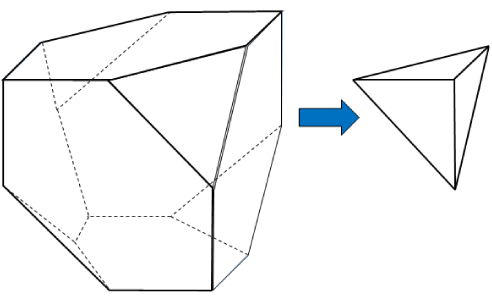
したがって、この立体の体積は、
| 2×2×2-1×1× | 1 | ×1× | 1 | ×4=7 | 1 | 3㎤ |
| 2 | 3 | 3 |
となります。
| ②答え | 7 | 1 | ㎤ | |||
| 3 |
複雑な立体は正多面体(正四面体・立方体・正八面体・正十二面体 ・正二十面体)の頂点からすい体を切り取って作られたものが多い です(よく問題に使われるサッカーボールの形は、正二十面体から作られています)。
見慣れない展開図が出てきましたら、正多面体をイメージしてみましょう。
ポイントが確認できるチャレンジ問題
問題
日本にあるJ商店では、アメリカにあるA牧場から毎月肉を一定量輸入して日本国内で売っています。J商店はA牧場に、肉の値段(肉の対価)と輸送費の合計(以下、この合計のことを「仕入れ費」ということにします。)を毎月支払っています。この支払いはすべてアメリカの通貨単位であるドルで行うので、日本円を用意しているJ商店の利益はドルの円に対する価値に左右されます。また、肉の値段は毎月ドルでは一定ですが、輸送費は原油価格の変動によりドルでも変動することがあります。
先月は1ドルは100円でした。先月は、仕入れ費の5割の利益を見込んで定価をつけて肉を完売しました。
今月は1ドルが90円になったので、原油高のため(ドルでの)輸送費が先月の2倍になったにもかかわらず、(円での)仕入れ費は先月の 93.6%ですみました。このため、円高還元セールとして先月の定価の3%引きの値段を肉につけましたが、完売したところ、利益は先月より95万円多くなりました。このとき、次の問いに答えなさい。
(1)先月の仕入れにおいて、肉の値段は輸送費の何倍でしたか。
(2)毎月支払っている肉の値段は何ドルですか。
(2009 開成中1)
※解答解説は次回掲載いたします。

