第13回 ゲームの達人~勝利の方程式~
今後の目次
第13回 ゲームの達人~勝利の方程式~ ← 今週はココ!
第14回 西暦問題いろいろ
第15回 数当て問題~ヒントの読み方~
今回は少し推理力を要するゲームの問題です。
ある決まったルールにしたがって行うゲームに実は必勝法があるとしたら?
このタイプの問題は論理的に考える力、いろいろな状況を調べ上げる力など受験算数に必要な力を要します。
まさに、「問題に条件(ヒント)が少なく、どう進めていいかわからないので難しい」問題と言えるでしょう。
今回は、どうすれば必ず勝てる「必勝法」がみつけられるか、そのポイントを説明してまいります。
ポイントが身につく問題実践講座
問題
次のようなゲームをします。
はじめに先生が、1以上2011以下の整数を1つ黒板に書きます。
先手は、その整数の1つのけたの数字を選んで(ただし0は除きます)、黒板の整数から、選んだ整数を引いた差に、黒板の整数を書きかえます。
後手は、その書きかえられた整数の1つのけたの数字を選んで(ただし0は除きます)、黒板の整数から、選んだ数字を引いた差に、黒板の整数を書きかえます。
これを交互にくり返して黒板に0を書いたほうが勝ちというゲームです。
(例)はじめに先生が黒板に21を書いた場合
先手が2を選び数字を19(=21-2)にする
後手が1を選び数字を18(=19-1)にする
先手が8を選び数字を10(=18-8)にする
後手が1を選び数字を9(=10-1)にする
先手が9を選び数字を0(=9-9)にすると、先手の勝ち
次の問いに答えなさい。
(1) はじめに先生が書いた整数が次の(あ)~(え)のとき、
先手必勝となるものには○、ならないものには×を書きなさい。
(あ)22 (い)15 (う)30 (え)41
(2) はじめに先生が黒板に書く1以上2011以下の整数のうち、先手必勝となる整数は全部で何通りありますか。
(2011 算数オリンピックファイナル)
【解くための考え方】
まずは、先ほどの問題を直接お子様に解かせてみてください。
どうでしたか?正解にたどりつけたでしょうか?
正解できなかった場合、どこまで解き進めることができたのかが重要です。
ゲームのルールはわかってもどうすれば勝てるのかがわかりにくいのではないでしょうか。
今後受験Dr.では、「難問攻略イメージde暗記ポイント」カードを作成する予定です。
今回は、その中から「規則のあるゲームの問題を解くための解法ポイント」を1つご紹介します。
今回使うポイント
- 条件に合ったゲームの必勝法がわからない
⇒【ポイントNo.29】「相手を負けさせる方法を考えよう」
【ポイントNo.29】「相手を負けさせる方法を考えよう」
わかりやすい「先手必勝となる最初の数字」を考えてみましょう。
一番わかりやすいのは、「1」です。
この場合は、先手が選べる数字は1しかありませんので、1-1=0となります。
数字を大きくしていくと、最初の数字が2でも3でも9でも先手必勝になることがわかります。
つまり、1ケタの数字のときはその数字をひくしかないので、必ず0になり勝つということです。
では、「10」はどうでしょう。
この場合選べる数字は1しかありませんので、10-1=9を黒板に書くことになります。
すると、後手は9-9=0となり後手が勝ちます。
つまり、10は後手必勝の数字ということになります。
「11」の場合を考えてみます。
先ほどの例から、黒板の数字が10で順番が回ってきたら必ず負けます。
先手は11-1=10を黒板に書きますので、結局先手が勝ちます。
「12」の場合も、2を選んで12-2=10とすれば先手が勝つことができます。
以上のことから、相手を必ず負けにするには、
10の倍数を書いて相手に順番を回す
ということになります。これが必勝法です。
(1)(あ)22のとき
先手は2を選び、22-2=20を黒板に書きます。
後手は2を選び、20-2=18を黒板に書きます。
ここで先手は8を選び、18-8=10を黒板に書きます。
後手は1を選び、10-1=9を黒板に書きます。
先手が9を選び、9-9=0を書けば勝ちです。
(い)15のとき、先手は5を選んで10を書けば必ず勝てます。
(え)41のとき、先手は1を選んで40を書けば必ず勝てます。
しかし、(う)30のとき、先手は30-3=27を黒板に書きます。
次に後手が7を選び27-7=20を黒板に書くと、後手が必ず勝つことができます。
(2)(1)の結果より、最初に書かれた数字が10の倍数のときは、後手が必ず勝ち、10の倍数でないときは先手が必ず勝ちます。
1から2011の間にある10の倍数の個数は、2011÷10=201あまり1より201個あります。
したがって、10の倍数でない数字は2011-201=1810個となります。
このようにゲームの必勝法と必ず負ける「必敗法」は表裏一体であるということです。
つい、勝つことばかりに目が行きますが、どうなれば負けてしまうのかを考え、相手がそのようになることを考えるのがポイントです。
【正解】
(1)(あ)○ (い)○ (う)× (え)○
(2)1810通り
開成・筑駒・灘の問題で今日のポイントを使う
問題 2006 灘中(2日目)4
図のような箱とボールを準備し、4つの箱にボールを1つずつ入れて、A君とB君の2人が次の(ア)、(イ)、(ウ)のルールにしたがってゲームをする。

(ア) 下の表のはじめから指示にしたがって矢印方向に進む
(イ) 取り出したボールはどの箱にももどさない
(ウ) 下の表のおわりまで進んだとき、最後のボールを取り出した者を勝ちとする
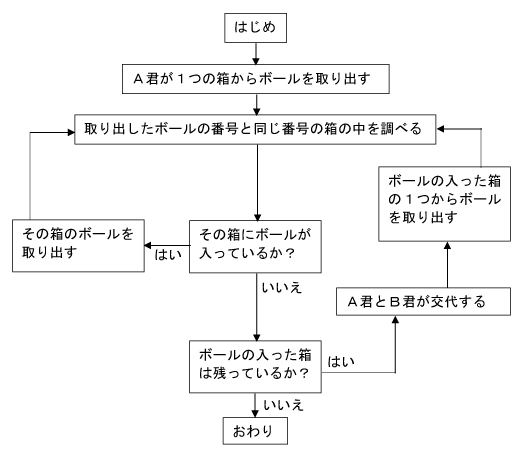
たとえば下の図のようにボールを入れたとき、A君が2の箱を選ぶと、②のボールが取り出され2の箱は空になるのでB君と交代し、
B君が1の箱を選ぶと、③、④、①の順にボールが取り出されておわりまで進み、B君の勝ちとなる。
次の各問いに答えなさい。
(1) 1から4まで番号のついた4つの箱に1から4まで番号のついた4つのボールを1つずつ入れる方法は全部で何通りありますか。
(2) (1)のうち、A君が4つのボールをすべて取り出して勝つようなボールの入れ方は全部で何通りありますか。
(3) (1)のうち、B君が勝つようなボールの入れ方は全部で何通りありますか。
【解説】
(1)
1、2、3、4の順に箱にボールを入れていくとすると、
1の箱に入れるボールの選び方は4通り
2の箱に入れるボールの選び方は3通り
3の箱に入れるボールの選び方は2通り
4の箱に入れるボールの選び方は1通りなので、
4×3×2×1=24
答え 24通り
(2)
A君が4つのボールを全て取り出して勝つ、ということはB君に1度も順番を回さない、ということになります。
(自分の順番のときには少なくとも1個はボールを取り出すので)←ポイントNo.29
B君に順番が回るのは、取り出したボールの数字と箱の数字が同じときです。
したがって、4つの箱すべて箱の数字と入っているボールの数字が異なるときになります。
表にして調べてみましょう。
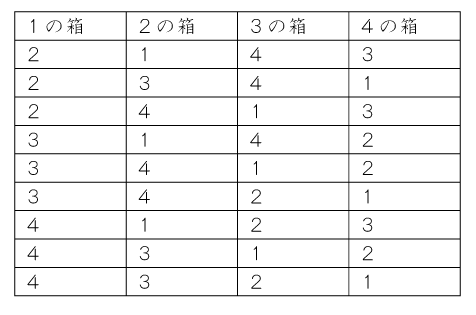
このうち、「2143」の場合は、
箱2から①を取る⇒箱1を見る⇒②を取る⇒箱2を見ると空⇒B君に交代
となるため問題の条件に合いません。
「3412」「4321」もこれと同じことがおこるので、この3つを除いた6通りが答えになります。
答え 6通り
(3)
B君が勝つ場合を考えると、
(ア)A君が1個取って交代⇒B君が残り3個取って勝ち
(イ)A君が2個取って交代⇒B君が残り2個取って勝ち
(ウ)A君が3個取って交代⇒B君が残り1個取って勝ち
(エ)A君が1個取って交代⇒B君が1個取って交代⇒A君が1個取って交代⇒B君が1個取って勝ち
という4通り考えられます。
それぞれの場合についてボールの入れ方を考えます。
(ア)の場合
箱と同じ数字のボールが入っている箱が1箱だけあり、残り3箱の数字と入っているボールの数字が同じではない場合です。
例えば、箱1に①が入っている場合を考えます。
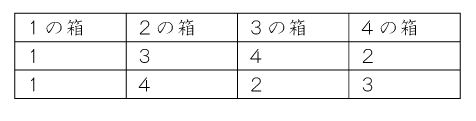
以上2通りになります。
これは2の箱が同じとき、3の箱が同じとき、4の箱が同じときでも2通りずつになりますので、
2×4=8通りになります。
(イ)の場合
(1)で出てきた「2143」の場合がこれに該当します。
つまり、箱の数字と入っているボールが2組逆になっている状態です。
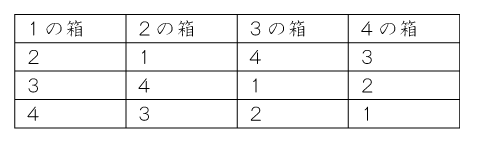
表より3通り入れ方があります。
(ウ)の場合
これは(ア)の場合と入れ方は同じになります。
箱との数字が等しいボールを選べば(ア)の場合になり、等しくないボールを選べば(ウ)の場合となります。
(エ)の場合
全て1回ずつボールを取って交代していますので、全ての箱で箱の数字と入っているボールの数字が等しい場合になります。
そのような入れ方は1通りになります。
したがって、8+3+1=12通りが答えとなります。
答え 12通り
前回のチャレンジ問題の答え
問題
3けたの整数のうち、次の条件を満たすものを「良い整数」とよぶことにします。
条件:3けたの整数を2つの整数に分けてその和を考えると、常にもとの整数の約数になっている。
(例)330は3と30に分けても、33と0に分けても和が33になり、330の約数になっています。
このため、330は「良い整数」となります。
ですが、702は7と02に分けた場合は7+2=9となり、702の約数になりますが、70と2に分けてしまうと、70+2=72は702の約数にはなりません。
よって、702は「良い整数」ではありません。
一の位が0でない「良い整数」を4個求めなさい。
(2010 算数オリンピックファイナル)
【解説】
3けたの整数をABCと表します。この記号を用いて、問題文の条件を式にします。
(AB+C)がABCの約数である、ということは
ABCが(AB+C)の倍数である、ということになります。
それは、ABC=(AB+C)×○ と表せます。
また、ABCはAB×10+Cとも表せますので、
AB×10+C=(AB+C)×○ になります。
そして、(AB+C)=(AB+C)×1という式との差を考えます。
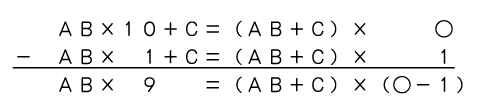
ここで、Cは0ではないので、ABとAB+Cは異なる数になります。
したがって、(AB+C)は9の倍数、という関係が見つかりました。
AB+Cは11以上108以下の倍数です。場合分けして考えていきます。
★AB+C=18のとき
AB×9=18×(○-1)=2×9×(○-1)
より、ABは2の倍数になります。
あてはまるABとCの組合せは、
(10、8)(12、6)(14、4)(16、2)です。
★AB+C=27のとき
AB×9=27×(○-1)=3×9×(○-1)
より、ABは3の倍数になります。
あてはまるABとCの組合せは、
(18、9)(21、6)(24、3)です。
以下、AB+C=36のときABは4の倍数になりますので、
(28、8)(32、4)
AB+C=45のときABは5の倍数になりますので、
(40、5)
AB+C=54のときABは6の倍数になりますので、
(48、6)
AB+C=63のときABは7の倍数になりますので、
(56、7)
AB+C=72のときABは8の倍数になりますので、
(64、8)
AB+C=81のときABは9の倍数になりますので、
(72、9)
AB+Cが90、99、108になるときは条件を満たす数字はありません。
これで14個まで絞れましたので、あとは表を使って調べましょう。
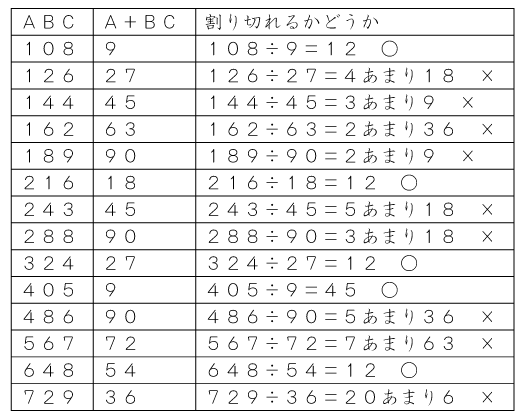
したがって、答えは○のついた5つの数字になります(このうちの4つを答えれば正解です)。
答え 108、216、324、405、648(のうち4つ)
今日のポイントを使って問題にチャレンジ!
問題
3枚の皿に石がそれぞれ1個、4個、5個のっています。
その皿からA君、B君の順に交互に石を取っていくゲームをします。
ルールは次のようになります。
・自分が取る順番のときは、石の残っているいずれか1枚の皿から1個以上の石を取る
・最後の石を取った方が勝ち

最初の石の状態を(1、4、5)と表します。
例えば、最初にA君が5個の石ののっている皿から3個の石を取ったとき、残りの石の状態は(1、4、2)となります。
次の各問いに答えなさい。
(1) A君が取る順番のとき、残りの石の状態が(0、2、2)となっていたなら、必ず勝つ方法があるのはA君、B君のどちらですか。
(2) A君が取る順番のとき、残りの石の状態が(1、3、3)となっていたなら、必ず勝つ方法があるのはA君、B君のどちらですか。
(3) このゲームは正しい手順で行うと、先手、後手のどちらかに必勝法があります。必勝法があるのは先手A君、後手B君のどちらですか。
(2011 高輪 改題)
※解答解説は次回掲載いたします。

