第9回 立体図形必勝法②(角すいの切断)
今後の目次
第9回 立体図形必勝法②(角すいの切断) ← 今週はココ!
第10回 立体図形必勝法③(立方体の複数切断)
第11回 調べる立体図形・サイコロ
今回は立体の切断です。立体の切断は難関校でよく出題されるテーマで、切断する際に通る点が与えられ、①どのような切断面になるのか、②切断された立体がどのような形で体積はいくつになるのか、が問われます。
前回の影の問題同様、平面上で立体図形の切断の様子を捉えるのは難しくテクニックが必要です。
しかし、このテクニックさえ身につけられれば多くの問題を解くことができるようになります。
また、切断についても昔は立方体や直方体が中心でしたが、今では三角すい・四角すい・六角柱と様々な立体が題材になりますし、同じ立体を複数回切断する問題もあります。
今回は、四角すいの切断を題材に、切断面の求め方や体積の求め方のポイントを説明してまいります。
ポイントが身につく問題実践講座①
問題
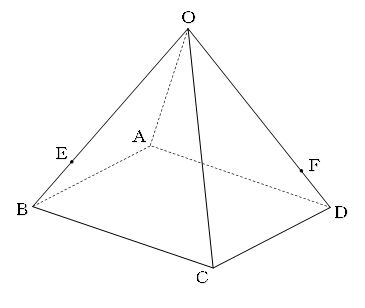
図の立体は正四角すいといい、底面が正方形で、OA、OB、OC,ODの長さはすべて等しい。
また、E、FはそれぞれOB、ODを3:1の比に分けている。
3点A、E、Fを通る平面と辺OCとの交点をGとする。
GはOCを : の比に分けている。
ただし、角すいの体積は
| (底面積)×(高さ)× | 1 | |
| 3 |
で求められる。
(2003 灘中(一日目)15①)
【解くための考え方】
まずは、先ほどの問題を直接お子様に解かせてみてください。
どうでしたか?正解にたどりつけたでしょうか?
正解できなかった場合、どこまで解き進めることができたのかが重要です。
切断の問題では、切り口(切断面)が立体図形に描けたかどうかがポイントです。
今後受験Dr.では、「難問攻略イメージde暗記ポイント」カードを作成する予定です。
今回は、その中から「切断面を上手く描いていくためのポイント・切断された立体の体積を求めるためのポイント」を合計4つご紹介します。
今回使うポイント
- 切断面の図が上手く描けない①
⇒【ポイントNo.20】「交点は対角・垂直切りで解決」
【ポイントNo.20】「交点は対角・垂直切りで解決」
まずは、立方体の切断と同様に同じ面にある2つの切り口の点を結びましょう。

これ以上切り口を結ぶことはできません。
立方体の切断の場合、向かい合う
平行な面では切り口の線も平行になる、という特徴を使って書き進めることができました。
しかし、角すいの場合向かい合う側面(例えば三角形OABと三角形OCD)は平行ではありませんので、この方法が使えません。
そこで、底面の対角線に沿って垂直に角すいを切断して考える、という新たな方法を取り入れます。
この四角すいを、三角形OBDを通る平面で切断します。
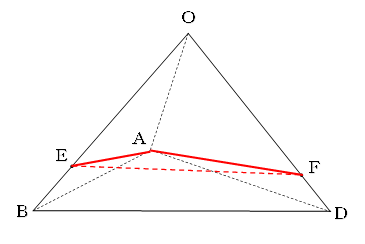
すると、直線EFが切り口の一部になっていることがわかります。
OE:EB=OF:FD=3:1より、三角形OBDと三角形OEFは相似形です。
底面の四角形ABCDは正方形なので、OからBDに垂直に下ろした直線とBDとの交点はBDの真ん中の点Pになります。

OPとEFの交点をQとすると、
OQ:QP=3:1、EQ:QF=1:1になります。
次にこの四角すいを、三角形OACを通る平面で切断します。
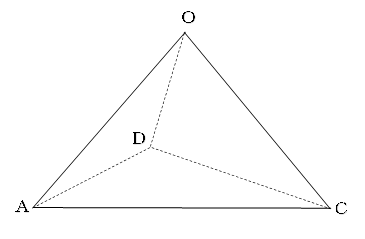
四角形ABCDは正方形なので、BDの真ん中の点PはACの真ん中の点でもあります。
そこで、直線OPと点Qを書き加えます。。
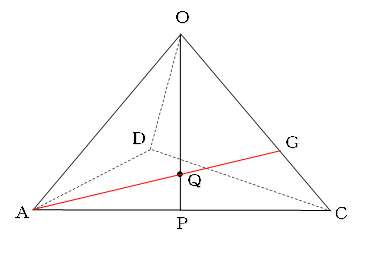
すると、AもQも切り口の一部の点になりますので、AQの延長線とOCの交点がGになることがわかります。
あとは三角形OAC上で考えます。
AGの延長線と、Oを通りACに平行な直線との交点をRとします。
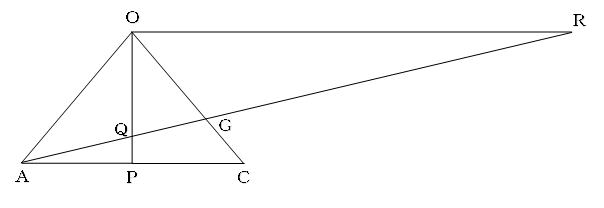
AP=①とすると、三角形QAPと三角形QROが相似形で、OQ:QP=3:1より、AP:RO=1:3となり、OR=③になります。
また、三角形GACと三角形GROも相似形で、AC:RO=CG:GOとなります。
AC=②より、CG:GO=2:3となります。
【正解】
3:2
ポイントが身につく問題実践講座②
問題
1辺の長さが6㎝の正三角形を4つはり合わせて、下の図のような立体を作りました。
点Pは辺AD上、点Qは辺AB上、点Rは辺CD上にあり、AP=2㎝、BQ=2㎝、CR=3㎝です。
3点P、Q、Rを通る平面でこの立体を切り、2つの立体に分けました。
3点P、Q、Rを通る平面が辺BCを切る点をSとすると、BSは何㎝になりますか。
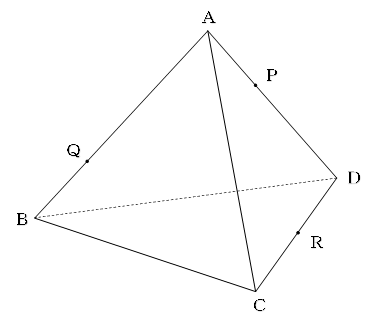
(2012 慶應義塾中等部 改題)
【解くための考え方】
まずは、先ほどの問題を直接お子様に解かせてみてください。
どうでしたか?正解にたどりつけたでしょうか?
正解できなかった場合、どこまで解き進めることができたのかが重要です。
先ほどの問題と異なり、三角すいには対角線がないのでポイントNo.20が使えません。
その場合の新たなポイントが次のポイントNo.21です。
今回使うポイント
- 切断面の図が上手く描けない②
⇒【ポイントNo.21】「切り口の延長線上に新たな交点」
【ポイントNo.21】「切り口の延長線上に新たな交点」
底面が三角形の場合、対角線がありませんので、切り口の線を延長し、新たな交点を見つけ出す方法が良いでしょう。
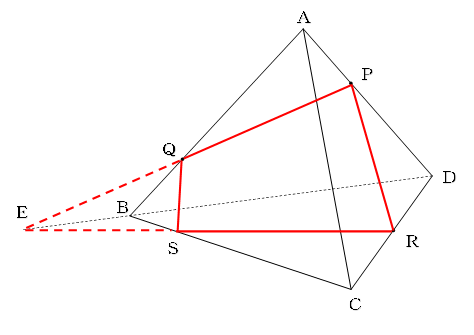
まずは、同じ面にあるPとQ、PとRを結びます。
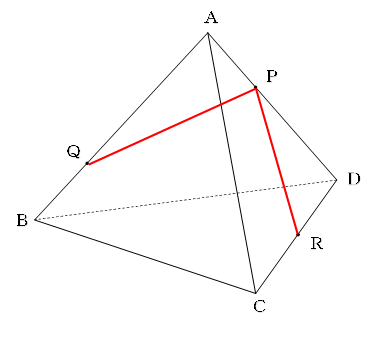
PQの延長線とBDの延長線の交点をEとします。
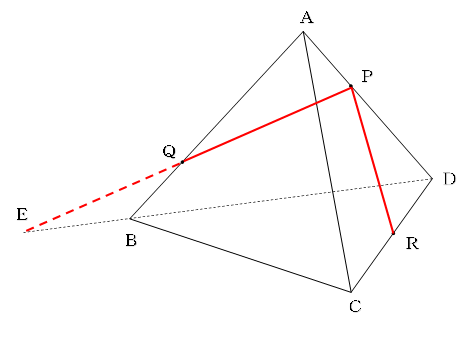
すると、EとRは同じ面上にありますので、切り口として結ぶことができ、ERとBCの交点が求める点Sになります。
BSの長さを求めるために、三角形ABDと三角形BCDの図を描いて考えます。
このあたりは、第8回立体図形必勝法①(影)で説明したポイントNo.19「立体は上・横の2方向で見る」と同じ考えによるものです。
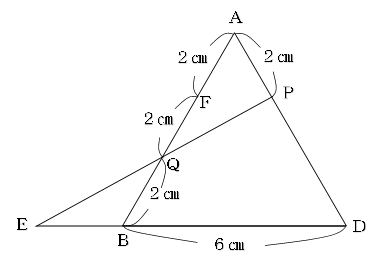
Pを通り、BDと平行な直線とABの交点をFとします。
三角形APFと三角形ADBが相似形なので、AB:AF=BD:FP=3:1となり、AF=FP=2㎝です。
また、三角形QPFと三角形QEBも相似形になり、FQ:QB=FP:BE=1:2となります。
したがって、BE=2㎝になります。
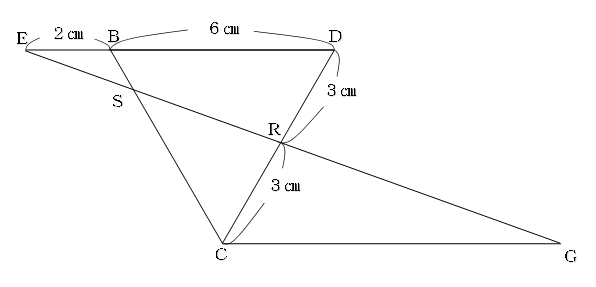
Cを通り、BDと平行な直線とERの交点をGとします。
三角形REDと三角形RCGが相似形なので、RD:RC=ED:GC=1:1となり、CG=8㎝です。
また、三角形SEBと三角形SGCも相似形になり、EB:GC=2:8=1:4より、SB:SC=1:4になります。
これで、BSの長さを求めることができます。
【正解】
1.2㎝
ポイントが身につく問題実践講座③
問題
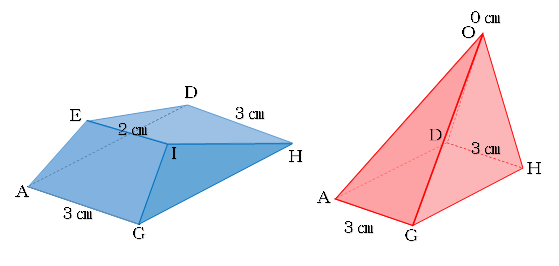
下の図は、底面が正方形で、4つの側面がすべて正三角形の四角すいで、
(OEの長さ):(EAの長さ)=2:1
(OFの長さ):(FBの長さ)=2:1 である。
この四角すいを面CDEFで切ったとき、下側の立体の体積は、もとの四角すいの体積の 倍になります。
ただし、角すいの体積は
| (底面積)×(高さ)× | 1 | |
| 3 |
で求められる。

(2002 灘中(一日目)15①改題)
【解くための考え方】
まずは、先ほどの問題を直接お子様に解かせてみてください。
どうでしたか?正解にたどりつけたでしょうか?
正解できなかった場合、どこまで解き進めることができたのかが重要です。
体積の場合、公式はありますが底面積や高さが求められないことがほとんどです。
そこで、体積を求める上で重要な2つのポイントを説明いたします。
今回使うポイント
- 切断した立体の体積が求められない①
⇒【ポイントNo.22】「角すいのてっぺんは辺の比の積」 - 切断した立体の体積が求められない②
⇒【ポイントNo.23】「垂直切断で切断三角柱を作ろう」
【ポイントNo.22】「角すいのてっぺんは辺の比の積」
このポイントは、平面図形の面積比で出てくる内容を立体図形に発展させたものです。
段階的に説明していきます。
① 頂点を共有する三角形の面積比は、左右の辺の比の積になる。

| 三角形OAB× | OC | × | OD | |
| OA | OB |
=三角形OCD
② 頂点を共有する三角すいの体積比は、3つの辺の比の積になる。

| 三角すいOABC× | OD | × | OE | × | OF | |
| OA | OB | OC |
=三角すいODEF
この2つは重要です。ぜひおぼえておきましょう。
では、問題のような四角すいはどうなるでしょうか。
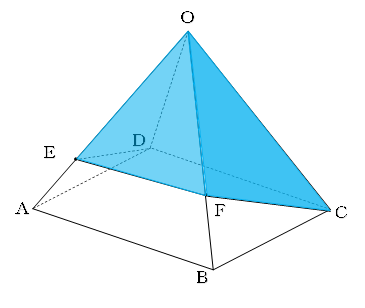
先ほどの三角すいと同様に考えて、
| 四角すいOABCD× | OE | × | OF | × | OC | × | OD | |
| OA | OB | OC | OD |
=四角すいOEFCD
になるとは限りません。
四角すいは底面の形や切断面の位置によって、この公式があてはまらない場合があります。
そこで、公式が使える三角すいに切り分けることで対応していきます。
四角すいOABCDを対角線BDに垂直な面で2つに分けます。
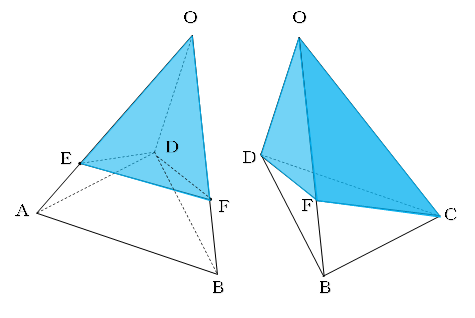
これにより、
| 三角すいOABD× | OE | × | OF | × | OD | |
| OA | OB | OD |
=三角すいOEFD
| 三角すいOBCD× | OF | × | OC | × | OD | |
| OB | OC | OD |
=三角すいOEFD
になります。
三角すいOABD,OBCDはともに
| もとの四角すいOABCDの体積の | 1 | |
| 2 |
になりますので、
| 三角すいOEFD | = | 1 | × | 2 | × | 2 | × | 1 | = | 2 | |
| 2 | 3 | 3 | 1 | 9 |
| 三角すいOFCD | = | 1 | × | 2 | × | 1 | × | 1 | = | 1 | |
| 2 | 3 | 1 | 1 | 3 |
したがって、四角すいOEFCDの体積は
| 2 | + | 1 | = | 5 | 倍になります。 | ||
| 9 | 3 | 9 |
求めるのは下側の体積なので、全体(1倍)から引いて求めましょう。
そして、体積の求め方にはもう一つの方法があります。
そちらを次のポイントで説明します。
【ポイントNo.23】「垂直切断で切断三角柱を作ろう」
三角柱をある平面で切断した、「切断三角形」(断頭三角柱と教える場合もあります)には、体積の公式があります。
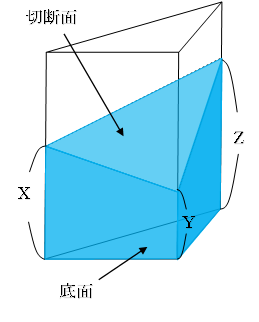
切断三角柱の体積
底面積×3か所の高さの平均
底面積×(X+Y+Z)÷3
この形を使うためには、3つの高さの直線がすべて平行であり、底面と高さが垂直に交わっている、という2つの条件を満たす必要があります。
では、問題の立体を見てみましょう。
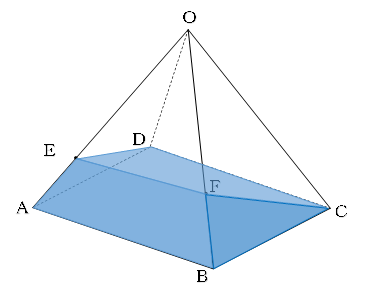
ABとDCとEFが平行なので、この3つが高さになりそうです。
しかし、AB・DC・EFはどれも面ADE,面BCFとは垂直に交わっていません。
つまり、この立体は切断三角柱ではありません。
そこで、「鳴かぬなら鳴かせてみようホトトギス」ではありませんが、
「切断三角柱でなければ切断してみよう」と発想します。
この立体を3つの高さに垂直な面で切り分けます。
お寿司の太巻きを真ん中で2つに切り分けるイメージです。
ABとDCの真ん中の点をそれぞれG、Hとし、O・G・Hを通る面で切断します。
そして、OGとEFの交点をIとします。
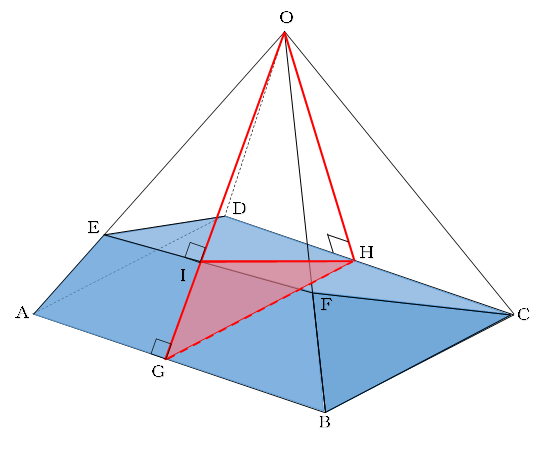
三角形OAB、三角形OCDはともに正三角形なので、OGとAB、OHとDCは垂直に交わることになります。
そして、ABとEFが平行なので、OIとEFも垂直に交わります。
これで、切断三角柱の条件が整いました。
この切断をすることで、もとの立体である四角すいOABCDも、2つの切断三角柱に切り分けられています。
AB=6㎝とすると、AG=3㎝になります。
また、OA:OE=3:2より、EF=4㎝で、EI=2㎝になります。
まずは底面積を比べます。
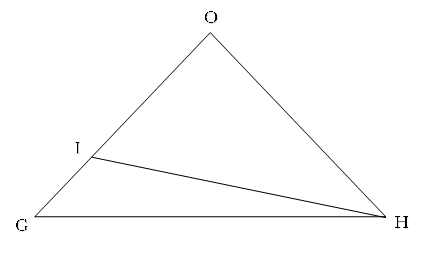
IG:OG=EA:OA=1:3より、
底面積の比は1:3です。
次に高さの平均を比べます。
(3+3+2)÷3:(3+3+0)÷3=4:3になります。
体積の比は、底面積の比と高さの平均の比の積になりますので、
1×4:3×3=4:9になります。
のように角すいの切断において、体積を求める方法は2種類あります。
どちらの方法を使えば良いのか?ですが、
1つの頂点を共有する「~すい」の立体である⇒ポイントNo.22
平行な直線が3本ある⇒ポイントNo.23
が一つの目安になります。
今回のポイントは立方体の切断でも使うことができますので、開成・灘・筑駒を目指す受験生はぜひ身につけておきましょう。
【正解】
| 答え | 4 | 倍 | ||
| 9 |
前回のチャレンジ問題の答え
問題 2009 灘中(1日目)12
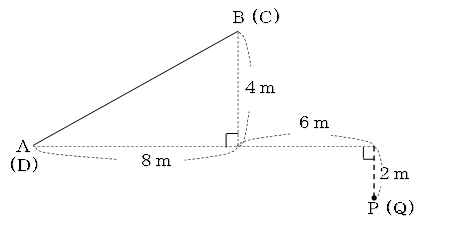
図1のように、平らな地面に3点A、B、Pがあり、高さ3mの長方形の壁ABCDと高さ9mの柱PQが、地面にまっすぐ立っている。
これらを真上から見たものが図2である。
柱の先端Qの位置にある電灯で壁ABCDを照らしたとき、地面にできる壁の影の面積を求めなさい。
ただし、電灯の大きさや壁の厚さは考えないものとする。
図1

図2
【解説】
壁を外し、柱ADとBCだけ残します。
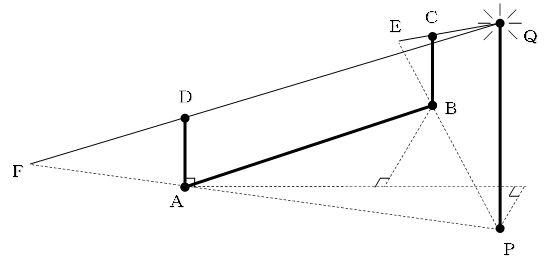
QからC,Dを通り地面と交わる点が、C,Dの影です。
その点をそれぞれをE、Fとします。
地面にできる壁の影は、四角形ABEFになります。

これを上から見た図で面積を考えていきます。

すると、三角形PABと三角形PFEが相似形になります。
相似比を求めるために横から見た図を描きます。
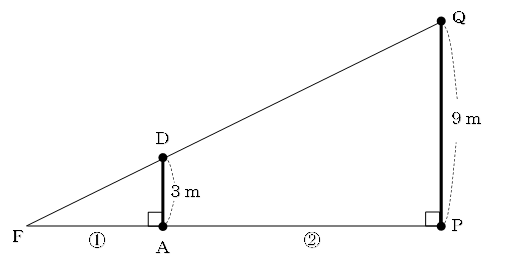
三角形FADと三角形FPQが相似形で、相似比はAD:PQ=1:3
になります。したがって、FP:AP=3:(3-1)=3:2です。
先ほどの上から見た図で、三角形PABと三角形PFEの相似比は、
PA:PF=2:3より、
面積の比は、三角形PAB:三角形PFE=2×2:3×3=4:9になります。
よって、三角形PABと四角形ABEFの面積の比は、
4:(9-4)=4:5になります。
そこで、三角形PABの面積を求めます。
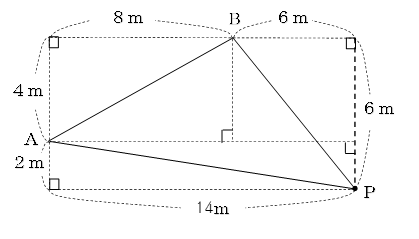
14×6-(14×2+4×8+6×6)÷2=36㎡
したがって、影の面積は、
| 36× | 5 | = | 45㎡です。 | |
| 4 |
答え 45㎡
今日のポイントを使って問題にチャレンジ!
問題
図のように四角すいの各辺の長さを8㎝とします。
さらに、この立体を下図の3点X、Y、Zを通る平面で切断し、上部(点Pをふくむ部分)を取り除きます。
このとき、残された立体を矢印の方向から見た図をかきなさい。
なお、切り口はエンピツで黒くぬりつぶすこと。
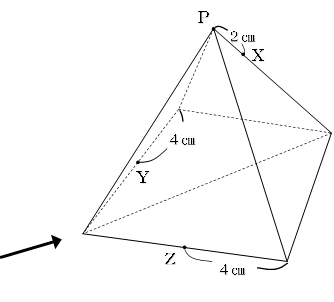
(2004 開成中 2(1))
※解答解説は次回掲載いたします。

