第１１回 調べる立体図形・サイコロ
今後の目次
第11回 調べる立体図形・サイコロ ← 今週はココ！
第12回 数の性質と場合の数の融合問題
第13回 ゲームの達人～勝利の方程式～
今回は身近な立方体であるサイコロを題材にした問題です。
サイコロの面には数字（目）があるため、その数字の組み合わせも考えさせる問題がよく出題されます。
その多くは場合の数として調べていく必要があります。
もちろん立体図形としてどのように転がるのかを考える力も必要になります。
その意味でサイコロの問題は、「②解答にたどり着くまでの作業量が膨大で、効率良い解き方が見つかりにくく難しい」問題と言えるでしょう。
今回は、立体図形の転がる問題をどのようにまとめていけばよいのか、そのポイントを説明してまいります。
ポイントが身につく問題実践講座
問題
下の図でスタートからゴールまでサイコロを転がしていきます。
スタートの位置では１の目を上にして、そのあとは一度も１の目が上にならないようにゴールする転がし方を点線に沿って書き入れなさい。
ただし、同じところを２度通ったり、遠回りをしてはいけません。
（１マスはサイコロ１つ分の大きさです）
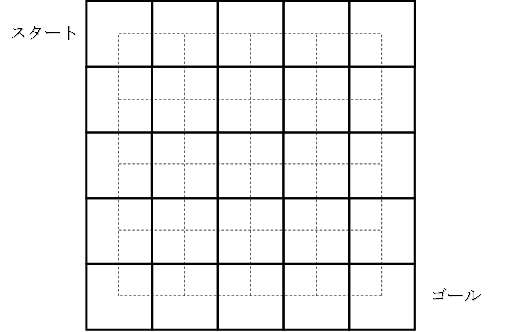
（1999 ジュニア算数オリンピックファイナル）
【解くための考え方】
まずは、先ほどの問題を直接お子様に解かせてみてください。
どうでしたか？正解にたどりつけたでしょうか？
正解できなかった場合、どこまで解き進めることができたのかが重要です。
サイコロが転がり、見える目を考える問題ではそれぞれの場所でどの目がどう見えていたかを記録していくことが大切です。
今後受験Dr.では、「難問攻略イメージde暗記ポイント」カードを作成する予定です。
今回は、その中から「サイコロが転がる問題を解いていくためのポイント」を２つご紹介します。
今回使うポイント
- どのように転がる様子を図にまとめれば良いかわからない
⇒【ポイントNo.26】「サイコロは上から押しつぶす」 - サイコロの動きの規則がよくわからない
⇒【ポイントNo.27】「側面を４つまとめて考える」
【ポイントNo.26】「サイコロは上から押しつぶす」
サイコロを上から見て、見える面の目の数に関する問題です。
与えられた図に上から見える目の数を書き込んでいけばよいのですが、
その都度どの目が上に来るかを考えていくと、どこかでミスしてしまいそうです。
そこで、立体をつぶしてたくさんの面を平面上に描くポイントNo.26を使います。
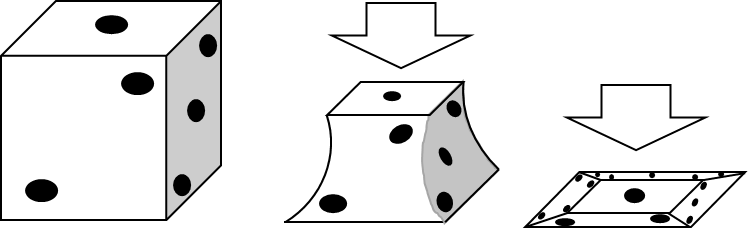
図のようにサイコロを上から押しつぶすと、上の面と側面の合計５つの面を表すことができます。
目を数字に変えて、
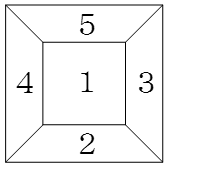
となります。
この図を使って、転がったときの目を記録します。
たとえば、右に転がると
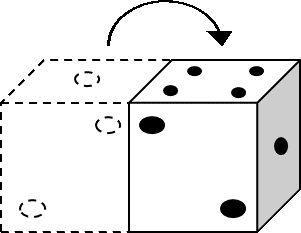
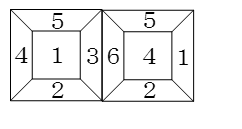となります。
【ポイントNo.27】「側面を４つまとめて考える」
スタート地点に１の目が上になるようにサイコロを置きます。
まずは、右方向にだけ転がした場合の目を考えます。
一番左と一番右は同じ目の組み合わせになっています。
このように、サイコロの側面は４面なので４回転がすと同じ目の組み合わせになります。
サイコロを転がす問題では、この４つずつを基準に考えていくと周期がわかることがよくあります。
今回、同じところを２回通ったり遠回りをしたりしないということは、
下方向に４回・右方向に４回転がすことになります。
そして、最初に下方向に転がしたときと最初に右方向に転がしたときは、線対称になる動き方が必ずありますので（下の図参照）、最初に右に転がした場合のみ考えます。
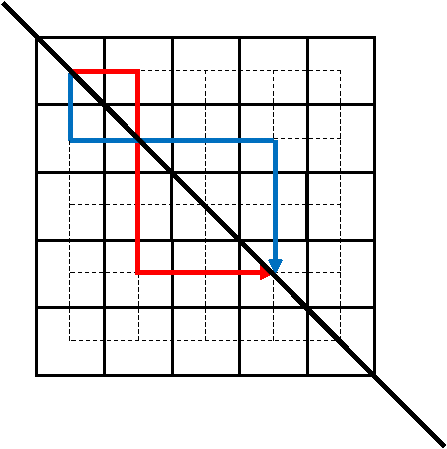
右に４回連続で転がすと１は上の面に出てしまうのでダメです。
また、３回連続で転がすと１は左の面に来ます。
このあと何回手前に転がしても、もう１回右に転がすと必ず１の面が上に来ますのでこれもダメです。
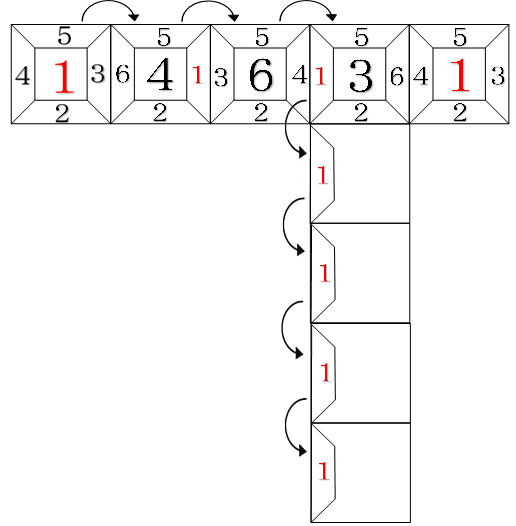
２回連続で右に転がした場合、手前に１回転がした時点で、１の目が後ろに来ます。
このあと右に何回転がしても次に手前に転がした時点で必ず１の目が上に来るので、これもダメです。
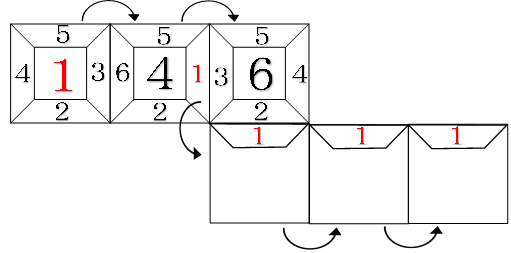
残ったのは、１回右に転がして次に手前に転がすときです。
何回手前に転がしても１は常に右の面に来ます。
この状態から２回連続で右に転がすと、１が左の面に来てしまい、次に右に倒したとき、１が上の面に来てしまいダメです。
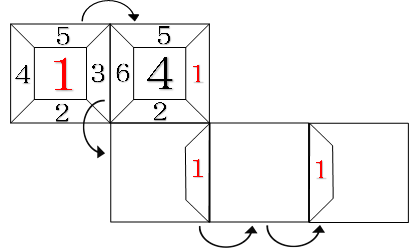
ではどうすればよいのでしょうか？
その答えは、「右に１回転がし、手前に数回転がしたあと、１回だけ右に転がし、１の面が底面にあるときに手前に転がし、１の位置を動かす」という方法になります。
何回手前に転がすかで場合分けして調べていきますと
１回右⇒３回手前→１回右⇒１回手前と動かしたときに、１の面が後ろに来ます。
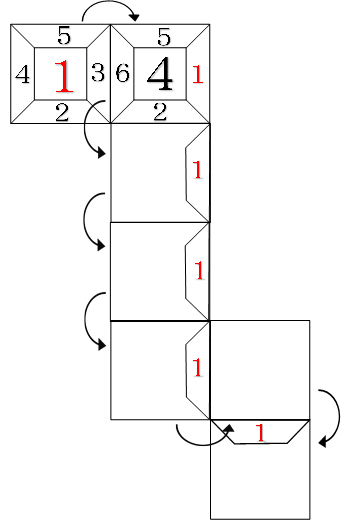
あと２回右に転がせば、１の目を上に出さずにゴールに着くことができます。
したがって、この進み方と右・手前を全て逆にした進み方の２通りが答えとなります。
【正解】
下の図のどちらか
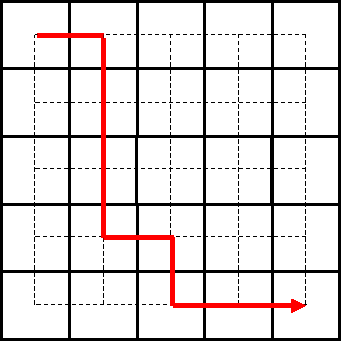
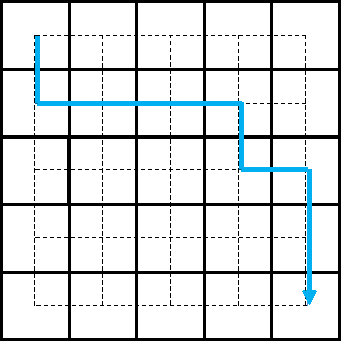
開成・筑駒・灘の問題で今日のポイントを使う
問題 2010 筑波大附属駒場中１
サイコロは向かいあう面の目の数の和が７になっています。
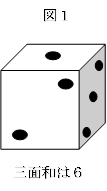
サイコロを図１のように見ると、３つの面を同時に見ることができます。
このときの見えている３つの目の数の和を『三面和』ということにします。
図１の状態の三面和は６です。
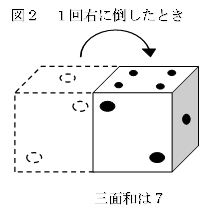
平面上に置いたサイコロを、底面のひとつの辺を軸に回転させて倒したときの三面和を考えます。
図２のように、図１の状態から右に１回倒したときの三面和は７です。
また、図３のように図１の状態から手前に１回倒したときの三面和は９です。
下の問いに答えなさい。
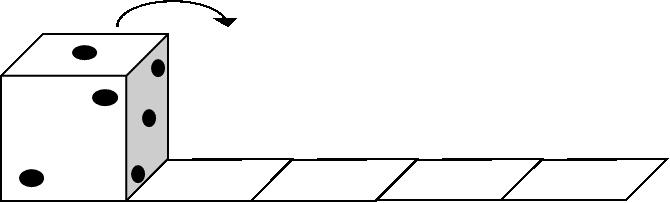
（１）サイコロを、右に続けて倒していきます。
図１の状態から２回倒したとき、図１の状態から３回倒したとき、図１の状態から４回倒したときの三面和をそれぞれ答えなさい。
（２）サイコロを、まず右に１回倒し、次に手前に１回倒し、次に右に１回倒し、次に手前に１回倒し、次に右に１回倒し、……というように倒していきます。
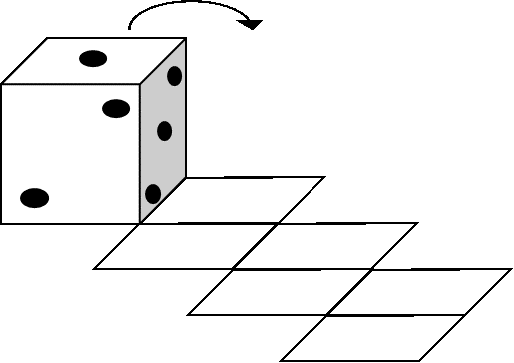
（ア）図１の状態から２回倒したとき、
図１の状態から３回倒したとき、
図１の状態から４回倒したときの
三面和をそれぞれ答えなさい。
（イ）図１の状態から、2010回倒したときまでの2011個の三面和の
合計はいくつですか。
【解説】
（１）サイコロを押しつぶした図を使って、転がしたときの目の様子を書いていきます。←ポイントNo.26
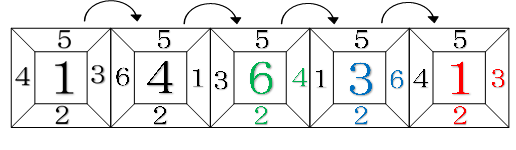
それぞれ上・正面・右にある数字の和が三面和になります。
２回倒したとき…１２
３回倒したとき…１１
４回倒したとき… ６
（２）（ア）こちらもサイコロをつぶした図を書いていきます。
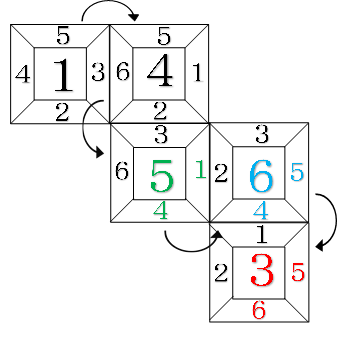
三面和はそれぞれ求めていきます。
２回倒したとき…１０
３回倒したとき…１５
４回倒したとき…１４
（イ）このようにとても多い回数や個数を考えるときは、何か規則や周期があると考えてよいでしょう。
サイコロの場合１～６までしかありませんので、今回は周期（繰り返し）を見つけます。
そこでさらに倒していきます。
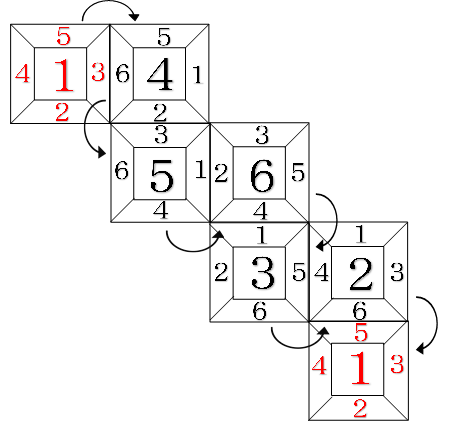
６回倒したときの目の組み合わせが最初の状態と同じになります。
また、このあと倒れる方向も最初と同じ右なので、この目の出方が続いていくことになります。
したがって、三面和は６、７、１０．１５、１４、１１と６つずつ繰り返します。
２０１１÷６＝３３５あまり１
（６＋７＋１０＋１５＋１４＋１１）×３３５＋６
＝６３×３３５＋６
＝２１１１１
前回のチャレンジ問題の答え
問題
図１のような立体を「三角すい」といい、その体積は、
（底面の三角形の面積）×（高さ）÷３
で求めることができます。
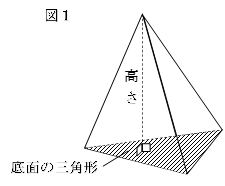
図２のような底面が正方形の直方体があります。
辺ＡＥを３等分する点をＡに近い方から順にＰ、Ｑとします。
図３は、この立体を真上から見た図と、真横から見た図です。
この立体から、まず三角すいＰＥＦＨを切り落とし、さらに三角すいＱＡＢＤのうち残っている部分を切り落としました。
図の１目盛りは１㎝であるとします。
でき上がった立体の体積を求めなさい。
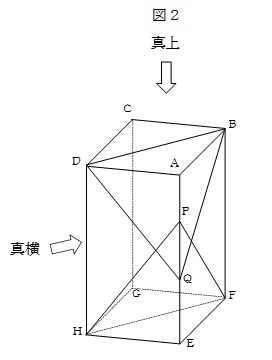
（２０１４ 開成中 ２（２））
【解説】
面ＢＤＱと面ＦＨＰが交わってできる交点を考えます。
まずは、三角すいＰＥＦＨを切り取るため、面ＦＨＰの切り口を描きます。
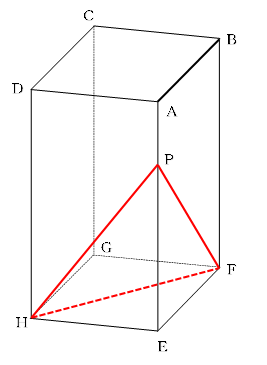
次は面ＢＤＱです。
ＤＱとＨＰが同じ面上に、ＢＱとＦＰが同じ面上にありますので、交点が２つ見つかります。
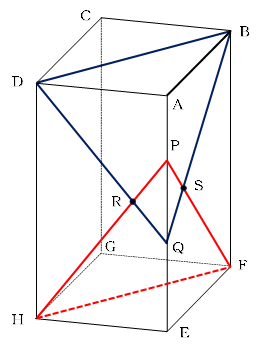
この２つの面で切り落とし、残る立体は下のような形になります。
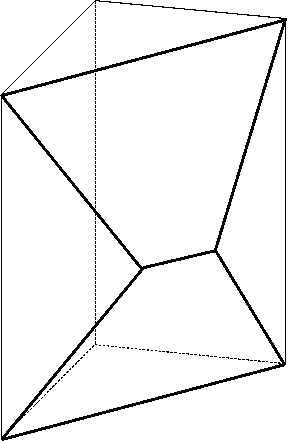
この立体の体積は、もとの直方体から三角すいを２つ切り落とし、「三角すいが重なった部分」の体積を戻す、という方法で計算します。
体積を戻すのは、２つ三角すいを切り落とすことで、１回だけ引けばよい体積を２回引いてしまっているからです。
図形を使った式にすると下のようになります。
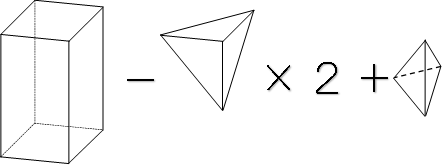
共通部分の体積を考えます。
Ｒ、ＳからＰＱに向かって垂直な線を引き、２つの三角すいに切り分けます。
２本の垂直な線の交点をＴとします。
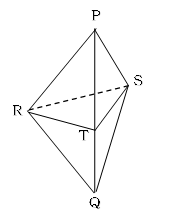
ＲＴとＴＱの長さは、面ＡＤＨＥ上で考えます。
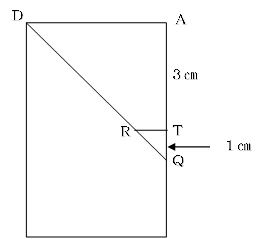
ＡＤ：ＴＲ＝ＡＱ：ＴＱ＝４：１（相似比）より、
三角すいＱＡＢＤと三角すいＱＲＴＳの体積の比は、
４×４×４：１×１×１＝64：１になります。
したがって、共通部分の体積は
| 三角すいＱＡＢＤの | 1 | × | 2 | ＝ | 1 | |
| 64 | 32 |
になります。
直方体 ４×４÷２×６＝48㎤
| 三角すい ４×２÷２×４× | 1 | = | 5 | 1 | ㎤ | ||
| 3 | 3 |
| 48－5 | 1 | × | 2＋5 | 1 | × | 1 | ＝ | 48－10 | 2 | ＋ | 1 | ＝ | 37.5㎤ | ||
| 3 | 3 | 32 | 3 | 6 |
答え 37.5㎤
今日のポイントを使って問題にチャレンジ！
問題
縦２列、横2007列のマスがあります。
図のように上の目の数が「１」の状態かのサイコロが左上のスタートのマス目から右下のゴールのマス目まですべらずに転がっていきます。
最短距離でゴールまで行ったときにサイコロの上の目の数が「６」になるような行きかたは何通りありますか。
サイコロは向かい合う面の数の和が７になります。
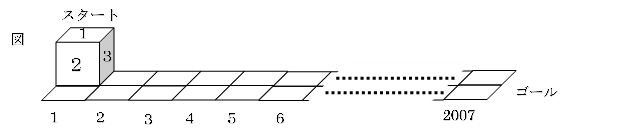
（2007 算数オリンピックトライアル）
※解答解説は次回掲載いたします。