私は、個別指導を専門に多くの生徒さんと接してきました。
算数、国語、理科、社会と各教科指導する中で、私が大切にしている3つの基本方針についてまずはご紹介させていただきます。

➀　生徒に自信とやる気を持たせる
➁　復習練習を徹底する
➂　学習時間を常に意識する

➀　生徒に自信とやる気をもたせる
「組分けテストは好きですか？」と生徒に聞くと、「嫌いだ。」と答える生徒が大半です。理由を聞くと、「成績が下がると親に怒られるから。」と答えていました。
このような親に言われて(怒られて)勉強するといった状況はあまり良くありません。もちろん、小学生のお子様は、自己管理がまだ上手くできないので強制力をもって保護者が管理する必要はあります。しかし、過度に管理してしまうと、言わなければ動けない状態に陥ってしまいます。これまでの受験生を見てきて、最後の最後で飛躍的に成績が伸びていくお子様は、自分で考え自分で行動できるお子様が多かったように感じます。その根底にあるのが自信とやる気です。自分は絶対合格できるという強い自信と歯を食いしばってでも努力するやる気を持つことで自分から動けるお子様を作ると考えています。
では、どうやって自信とやる気は身に着くのでしょうか。それは【成功体験】です。小テストなど身近なことで構いません。努力してその成果が表れた時にすぐにその頑張りを認めてあげましょう。するとお子様は、何か失敗した時でも成功体験を思い出して、「前とは何がちがったのだろう？」、「次は絶対成功させる」など、次の成功に向けてがんばれる原動力になります。そして、この成功体験の積み重ねが強い自信と自分自身を信じで頑張れるやる気を引き出します。
私は、生徒の自信とやる気を引き出すため、生徒に寄り添いながら進む道を示し、背中を押してあげたいと考えています。

➁　復習練習を徹底する
「応用問題は難しくて解けなかった」などの生徒からの声を良く聞きます。このできなかった問題が、初めて見る問題なのか学習したけど忘れてしまった問題なのかが重要になってきます。初めて見る問題はある程度は仕方ありません。しかし、学習したのに忘れてしまったことは問題です。学習したことは忘れずに定着させる、そのための授業を行います。
私は、【その週に学習した内容はその週のうちに、自力で正解できるまでやり込む】ことを基本としています。つまり、復習に力をいれます。また、生徒のレベルに合わせて解くべき問題を取捨します。
具体的には、問題を3回まわします。1回目は、学習してから2日以内に、まだ授業を覚えているうちに問題を解きます。2回目は、1回目で間違えた問題の解きなおしで、解答以外であれば授業ノートやテキストを見て調べてかまいません。だたし解く際は、ノートやテキストは見ずに解きなおしを行います。3回目は、2回目で間違えた問題の解きなおしで、解答を読んで理解した上で解答を見ずに解きなおしを行います。ここまでやれば3か月は記憶に残ります。忘れたころに各期別講習がありますので、その時に再度復習します。この復習中心の学習方法は、保護者の方の協力が不可欠です。保護者の方は解答を保管し、○付けを行っていただけると助かります。
どの問題を復習するか、問題選択はぜひプロの講師におまかせ下さい。

➂　学習時間を常に意識する
時間は有限です。ただ漠然と学習に取り組むのと時間を気にしているとでは作業の効率が変わってきます。
自宅学習をする際は、【ノートまたはプリントの表題に、日付と開始時間と終了時間】を記入してもらいます。たったこれだけで時間に対する意識や、効率、やる気が変わります。例えば、同じ量の問題がいつもは60分かかっていたのに、今日は30分で終わった場合、解くスピードが上がっていることが客観的にわかります。先生が傍にいなくても、時間が頑張ったお子様を評価してくれるのです。お子様もさらなる時間短縮を目指してがんばる動機になっていきます。ぜひ、保護者の方もノートなどを見て時間短縮ができた日には、お子様の頑張りを認めるようなお声がけをしてみてください。
私は、時間の意識付け以外にも、お子様の性格も考慮して楽しみながら学習意欲を高める工夫を行ってまいります。

算数は、➀計算力と➁記憶力の勝負と考えています。

➀　計算力
計算力を鍛え、計算スピードを上げることは、算数において必要なことは誰もが納得することだと思います。そして、計算力を鍛える方法としては、計算ドリルのようなテキストで毎日コツコツと計算問題を解いていかなければなりません。この計算力を鍛える作業が小学生のお子様にとっては退屈この上ない作業です。私も小学生のころ、単純作業である計算練習が苦手でした。しかし、あることでそれほど苦にならなくなりました。それが【タイムトライアル】と【習慣】でした。ストップウォッチをで、10題解く時間を毎日計測していました。当時はストップウォッチが珍しく、それを使いたいがために計算練習をしていたようなものでした。そのうち、計測時間が前日より短くなったかどうかで一喜一憂するようになりました。そして、この毎日のタイムトライアルが朝食を食べる、歯を磨くなどの日常習慣の一つなり、気づくと朝起きたら計算練習してから学校に行くことが当たり前の生活になっていました。今思うと習慣って恐ろしいなと思いました。 ただ漫然と計算練習するのは退屈です。楽しみを見つけてメリハリをつけると良いです。

➁　記憶力
ここで言う記憶力とは、理科や社会などで言われている用語の暗記のことではありません。【典型問題の解き方を暗記する】でということです。
私は、この典型問題をどのくらいストックできているかが算数の力だと考えています。一般的に難問と呼ばれている問題は、いくつかの典型問題が組み合わさったり、典型問題をひねったりして作られています。今まで解いた問題の中から、解き方の近い解法を思い出して試行錯誤していく。0から考え行くと時間が足りません。ベースとなる典型問題を素早く思い出せるかがカギになります。なので、6年生の夏休みが終わるまでに典型問題の解き方をしっかり暗記していきましょう。問題を見ただけで、即座に典型問題がいくつか思い出せるように暗記しましょう。

国語は、➀答えを本文から探す。➁正しい記述は模範解答の真似から。を基本方針に考えています。

➀　答えを本文から探す
国語は答えが本文に書いてあると良く言われます。その通りだと思います。設問を手掛かりに答えを本文から探す、宝さがしゲームです。ただし、答えが直接書いてあるものもあれば、情景やセリフや行動から推測しないといけないものまであります。また、設問から、どうやって答えを探すのか、探し方も決まっています。このように【設問を頼りに答えを探すやり方と本文から答えを見つけて適切な形に加工するやり方】を身につけることが国語の学習のポイントとなります。

➁　正しい記述は模範解答の真似から
記述問題で、正しい日本語が書けていないというお子様を良く見かけます。単なる本文の丸写しだったり、複数の文を無理やりつなげているため、主語・述語の関係が崩壊していたりと日本語になっていない文を書いてしまっています。これを改善する方法は、まずは上手な人のやり方を真似してみることです。ここでの上手な人とは模範解答です。模範解答はいろいろなこと考えられて練られた文章です。模範解答を読むことで、文法的な意味は分からなくても、美しい日本語の表現方法や論理的文章の展開などが何となく理解できてきます。その上で、【模範解答を模写しましょう。】何度も書いていくうちに自然と日本語の感覚が身に付き、文法的にも正しい文が書けるようになります。
「習うより慣れろ」のように、模範解答の模写は正しい記述の第一歩となります。

理科は、苦手単元に絞って学習することを基本方針に考えます。

理科は「生物」「化学」「物理」「地学」の4分野に分かれ、各分野の単元ごとに独立している特長があります。また、暗記分野と計算分野に分かれていてそれぞれ対策が違います。一見するとやることが多岐にわたり大変かと思いますが、そうではありません。算数のように、積み上げ型の単元構成でなく、単元が一つ一つ完結しています。なので、一つの単元の完成が比較的容易なため、短期間で点数を伸ばしやすい科目と思います。苦手単元が、暗記系なのか、計算系なのか、によって実際の学習方法は変わりますが、【苦手単元を重点的に克服すれば、全体の底上げ】につながると考えています。

社会は、点で覚えず、面で覚えることを基本方針に考えています。

社会は暗記科目と言われています。いかに用語を正確に、多く覚えるかがまずは重要となります。しかし、一問一答方式に暗記していくとどうしても忘れてしまうことがあります。そこで、点と点をつなげ、【色々な知識と関連づけながら面として覚えていきます。】例えば、江戸幕府を開いた人＝徳川家康、を暗記したとします。徳川家康と関連する知識を他にも紐づけます。徳川家康が勝利した関ヶ原の戦いは何年？＝1600年。徳川家康に関係の深い世界文化遺産はどこ？＝日光東照宮。など。授業では、関連した知識を質問しながら、ただ覚えるのでなく、地理・歴史・公民の全分野の知識と紐づけながら、忘れないように覚えることに重点を置きます。

【開成　2,021年　大問１(2)】
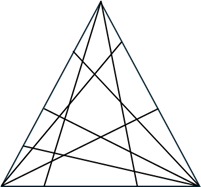
三角形の頂点を通る何本かの直線によって、その三角形が何個の部分に分かれるかについて考えます。ただし、3本以上の直線が三角形の内部の1点で交わることはないものとします。右の図のように、三角形の各頂点から向かい合う辺に、直線をそれずれ2本、2本、3本引いたとき、元の三角形は24個の部分に分けられます。
では、三角形の各頂点から向かい合う辺に、それぞれ2本、3本、100本引いたとき、元の三角形は何個に分けられますか。


➀　まずは、方針を考えよう。
いきなり数えたり書き出したりせず、まずは方針を考えます。「規則性」の問題ですので、何か規則がないか考えます。
ここでの注目ポイントは設問の条件です。「2本、2本、3本では24個」「2本、3本、100本では何個」とあるので、共通している「2本、3本」から1本ずつ書き足していって、三角形が何個ずつ増えるか調べていけばいいのでは、という方針が立ちます。ここに気付けば、後は手を動かして調べていきます。
➁　具体的に調べていこう。
図1のように、2本と3本の線を引いたとき、三角形は「12個」できます。

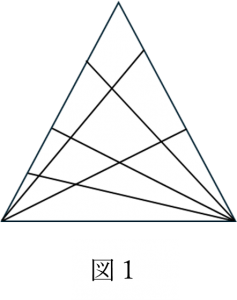
ここから図２のように1本線を引くと、交点が「5個」でき、新しく増える三角形が「6個」できます。

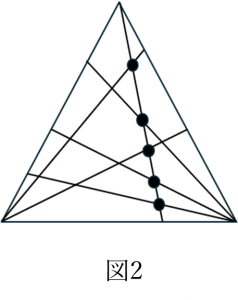
交点の数はどのように決まるのでしょうか？これは、図１で引いた直線の総数＝5本と交わっているからです。
また、交点が5個できれば、新しくできる三角形は5＋1＝6個できることがわかりました。
これのくり返しで、「2本と3本」の図形に新たに「100本」線を引けば、1本ごとに「6個」の三角形が新しくできることがわかります。
➂　答えを求めよう。
よって、元からある12個の三角形にあたらしくできる三角形を加えて、
　12＋6×100＝612個に分けられます。