指導方針

問題が解けるようになるために重要なことは、次の２点です。

１．原理を理解すること
問題に応じた公式や解き方のパターンが存在します。
公式がもつ意味や、解き方が持つ意味を理解し、解き方の前提となる仕組みを理解する。

２．手続きを習得すること
公式を用いる、補助線を引く、表を作って調べるなど、問題に適した手順を練習によってスムーズに実行できるようにする。

実際は、練習によって２．の手続きがスムーズにできていれば、それだけで点数は取れるようになります。
ただ、ここで安心することはできません。なぜなら１．の理解が伴っていないと、応用が利かず、時間がたつと忘れやすくなるからです。

基本の理解を徹底することで、記憶・定着の負担が小さくなり、基本の仕組みが共通している問題に対して知っていることを応用できるようになります。

そのために、以下のことを重視して指導していきます。

・基本の徹底をはかる
理解の部分が不十分だと、次の段階に進めません。
解けるようになって、生徒本人は自信もある。でも理解の部分は不十分なところは、積極的に基本に立ち返って押さえなおす。これによって、忘れない、応用が利くという最終目標につながる知識が入ります。

・生徒にとってのベストを考える。
問題文の条件を、式を立てて式だけで押していくのか、線分図を描くのか、表を描くのか。
基本的な部分は共通していますが、具体的な作業に入っていくと、生徒によってしっくりくるやり方が異なることもあるので、生徒が違和感を持たずに取り組める方法を優先します。

・達成感を持たせる
目の前の１問に集中し、正解したらともに喜ぶ。残念だった場合はともに悔しがり、次は正解するぞと気合を入れる。良い意味で一喜一憂し、間違えても落ち込まず、前向きな気持ちで取り組めるようにします。

基本の徹底がどのように実になっていくのかを、以下の指導実例にて示します。

指導実例１　平面図形

図形の折り返しにおける基本の徹底

問題
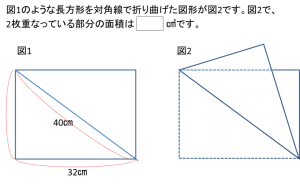
ooki-1
折り返しに関する基本事項として、

 １．移動前の図形と移動後の図形は合同
 ２．重なった部分は二等辺三角形

の２つを押さえ、すぐに活用できるようにします。
１は、折っただけなので、当たり前なのですが、重要です。
２について、平行線の性質を用いて説明しておきます。

まず平行線の錯角である○印の２角が等しくなります。
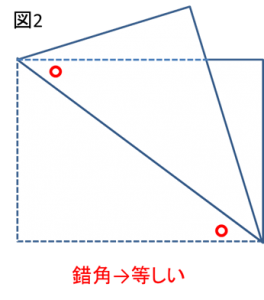
ooki-2
続いて、折り返し→合同により、○印の２角が等しくなります。
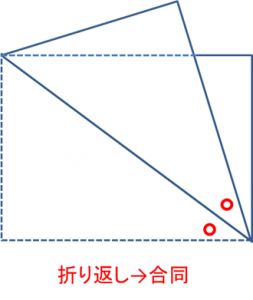
ooki-3
以上より、2枚重なった部分は二等辺三角形ということが分かりました。
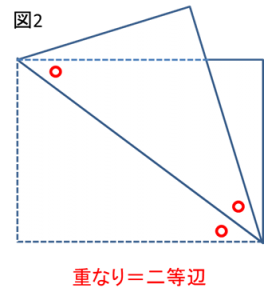
ooki-4

本問では、続いて直角三角形の相似を確認します。
重なり部分を、図のように２つの合同な直角三角形に分けます。色を付けた部分をイとします。

すると、○印の角が等しいことから、２つの直角三角形アとイが相似であることが分かります。
アは、有名な辺の比3：4：5の直角三角形です。
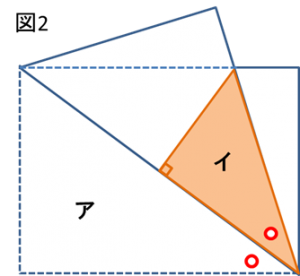
ooki-5
長方形の対角線は40cmでしたので、その半分が20cmであることを利用して、アの３辺の比をそのままイに適用すると、辺の長さが図のように求まります。
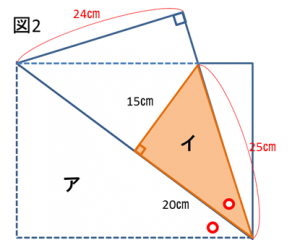
ooki-6
あとは、イの面積をもとめて２倍すれば、重なり部分の面積を求めることができますね。


折り返しの基本　①合同　②二等辺
を身につけておくと、有利に働くことがわかると思います。

指導実例２　時計算

時間に応じて２針の角度が変化する、という基本の徹底

普通の時計と設定を変えた時計の問題を例に、攻略法を考えます。御三家をはじめとする難関校では定番と言える頻出問題です。
なぜ特殊な時計が好んで出題されるかというと、原理の理解を伴わずに表面的に計算方法を覚えただけの受験生は対応できないからです。

問題

ある星では、1日が8時間で、1時間が40分です。この星の時計は次の図のようになっており、例えば、図1は3時ちょうど、図2は3時20分を表しています。下の問いに答えなさい。
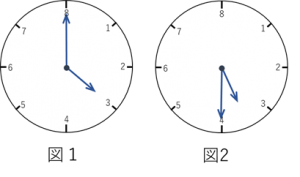
ooki-7
(1)3時32分のとき、長針と短針が作る角のうち、小さい方の角の大きさは何度ですか。
(2)長針と短針の作る角の大きさが90°となるのは1日で何回ありますか。
(3)現在4時16分です。次に長針と短針の作る角の大きさが128°となるのは何分後ですか。

まずこの星における時計を把握しましょう。
地球の時計とこの星の時計の基本データを表にまとめてみます。
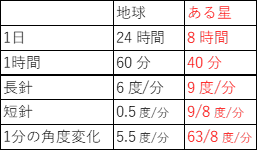
ooki-8
いつもの時計算に、ご当地仕様（この星）の数値を用いればよいことがわかりますね。

（１）
時計の短針と長針のなす角を求めます。地球の時計と同じ解き方ですが、設定（数値）だけ変えて動かします。
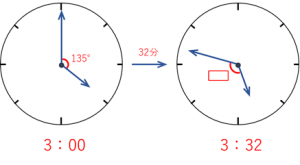
ooki-9
1分で63/8°変化するので、
32分では　63/8×32＝252°変化しました。
□＝252 ― 135＝117° と求められました。

（２）
短針を追い越す前と後で、90°になることが2回ずつ起こりそうですが…
表にまとめていきます。
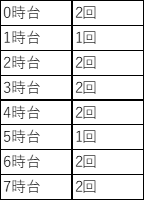
ooki-10
2時00分　は1時台と2時台の境目にあるため、1時台に90°となることは1回しかありません。
同様に、6時00分は6時台に入るため、5時台も1回。よって、合計＝14回。

（３）
4時16分の次に角度が128°になるのは、下の図のような時です。この時刻を求めて、4時16分の何分後になるかを答えればよいのです。
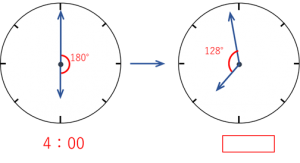
ooki-11
180°追いついて128°引き離すので、角度変化は
180＋128＝308°。それにかかる時間は、
308÷（63/8）＝352/9分
4時の352/9分後が4時16分の何分後かを求めて、
352/9－16＝208/9　分が求められました。

地球でも、他の星でも時計の原理は同じなので、１分の角度変化を用いるという基本を徹底することで、具体的には対照表を書くことで、目先の変化に惑わされずに攻略できる感じがつかめるのではないでしょうか。