〇公式は使いこなせてこそ意味がある　丸暗記はできるだけ減らそう
　算数や理科、さらに中学以降の数学では、様々な公式や法則、定理といったものが次々に現れます。例えば算数の速さの単元に絞っても、速さの3用法に始まり、旅人算の出合い・追いつき、流水算の上りと下りの速さ、通過算、時計算…と様々な問題とそれに対応する公式が各塾のテキストにまとめられています。もちろん、例えば旅人算を初めて学習するにあたり、「こうすれば解ける」という道筋がしっかりと示されているのは心強いでしょう。最初のほうに学習する問題は公式に当てはめていくだけで解ける簡単なものが多いので、公式さえ覚えておけばテストでもある程度点数は取れるはずです。しかし、何回か学習の回数を重ねていくうちに、問題のほうが単純な公式の当てはめでは解けないものに変わっていきます。5年後半～6年前半にかけて成績が下がっていくというのは、ここに大きな原因があるのではないかと考えます。
　これに対する対応法は、「公式を成り立ちからイメージし直す」ことです。例えば旅人算の出合いの公式は「（2人の間の距離）÷（速さの和）＝時間」になるわけですが、これを「（2人が進んだ距離の和）÷（速さの和）＝時間」ととらえ直すことで、折り返しての出会いの問題につなげやすくなりますし、そもそも「距離÷速さ＝時間」という速さの基本公式の拡張版ともとらえられるわけです。このような、「なぜその公式が成り立つのかを考え直して、使いこなしやすいよう再構築する」ことを行っていきます。

〇解き方は１つだけではない　広い視野で問題を見よう
　「問題を解く」という作業は、大きく３つのステップに分けられます。まず、「問題の意味を理解する」こと。問題文を正確に読むのはもちろんですが、その情報を自分なりにまとめたり、何を求めれば答えにたどり着くかを考えたりすることがこの段階に入ります。2つ目が「与えられた情報と既に分かった情報から次の情報につなげる方法を選ぶ」こと、そして3つ目が「選んだ方法で情報を処理すること」になります。3つ目はつまり計算の段階、1つ目は問題のレベルによって必要な内容が大きく変わってきます。どのような問題でも共通で必要になるのが2つ目の力で、ここを素早く終えることができるかどうかが問題全体を解くスピードに大きく関わってきます。現在私はしち塾で数学も見ているのですが、新しく学んだことを使おうとするあまりにもっと簡単な解き筋を見落とすというのは非常によくあることです。使える手法が増えてきた頃こそ、どの解法を使うかの選択は重要になります。生徒の状況にはよりますが、正解した問題であっても他の解き方はないか追及していくことで、問題に対する色々な見方を養っていきます。

武蔵中2023の問題3⃣を例とします。
（問）図において、２つの四角形ABCDとEBFGはどちらも正方形で、CF＝3cm、HG＝1.8cmです。
(1) BFの長さを求めなさい。
(2) 図の斜線部分の面積を求めなさい。


まずは必要な情報を図に整理していきます。この問題では、赤で書きこんだ直角３つと、正方形なのでBF=FGということが重要です。
この情報を書き込んだ時点で、BFの長さを求めるには直角三角形の相似を使いそうだというのが何となく見えてきます。そこで、その方針に向けた作業を行います。


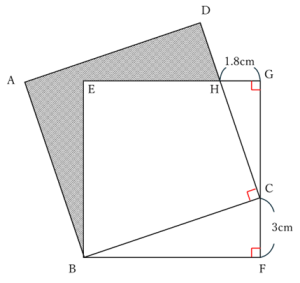
片方の直角三角形に〇✕の角を書きました。すると、点Cのまわりが180°になるため、もう片方の直角三角形も同じ〇✕の角になることになり、相似な三角形の組が見えました。FCとGHが対応する辺なので相似比は5：3になります


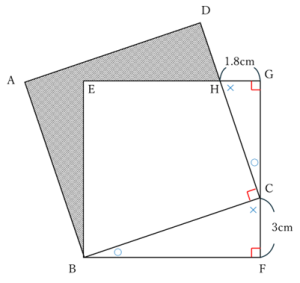
対応する辺の長さBFとCGを⑤、③とおいて、正方形であることから
⑤ ＝ ③ + 3cm
となり、求めるBFの長さは7.5cmとなります。


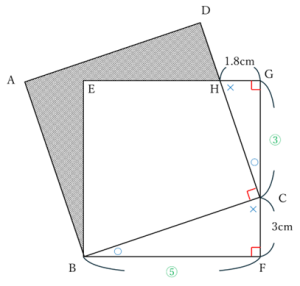
(1)は相似に気付けば楽な問題でしたが、(2)はどうでしょうか。まず求めたい図形の形が複雑なので、直接求めることはできません。とすると、正方形ABCDから四角形EBCHを引き算するような求め方になりそうです。四角形EBCHについては正方形BFGEから直角三角形２つを引けばよいとして、目標を正方形ABCDの面積を求めることとしましょう。
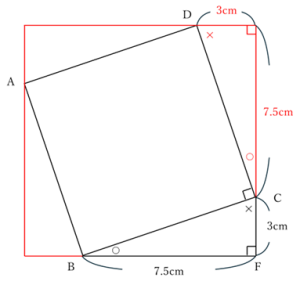
元の図から一部省略すると右図の黒線部になります。ここから、三角形BFCと合同な三角形を３つ正方形ABCDのまわりに足すと、1辺10.5cmの正方形ができます。ここから、正方形ABCDの面積は
10.5 × 10.5 – 3 × 7.5 ÷ 2 × 4 = 65.25㎠
と求まります。このように、「問題の条件からどのような考え方が使えるか」を意識させながら解くことで、似た問題を見たときに対応しやすくなります。

豊島岡2024第1回2⃣の化学計算を例とします。

（問）（要約・抜粋しています）　次の２つの反応をふまえ、実験を行いました。
反応１：

反応２：

実験：水酸化ナトリウムと炭酸水素ナトリウムを水に溶かして水溶液Aとした。水溶液Aに塩酸を少しずつ加えていき、できた二酸化炭素の体積を調べた。
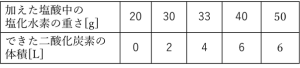
結果：

(2) 以下の➀、➁それぞれの水溶液にBTB液を加えたときの色として最も適切なものを答えなさい。
　➀　水溶液Aに塩化水素25g分の塩酸を加えた水溶液
　➁　水溶液Aに塩化水素40g分の塩酸を加えた水溶液
(3)(4) 水溶液Aに塩酸を少しずつ加えていくとき、はじめに反応１だけが起こり、水酸化ナトリウムがすべて反応したあとに反応２が起こるとします。このとき、水溶液Aをつくるために加えた炭酸水素ナトリウムと水酸化ナトリウムはそれぞれ何gですか。四捨五入して整数で求めなさい。

(3)(4)の文章に書いてありますが、はじめ塩酸を加えても二酸化炭素が発生しなかったという結果から、先に水酸化ナトリウムが反応し、その後に炭酸水素ナトリウムが反応していると想像できます。さらに、反応２から、炭酸水素ナトリウムとの反応が起きているときは、塩化水素3gに対して二酸化炭素2Lが発生することがわかるので、結果の解釈としては塩化水素27gまでは水酸化ナトリウムと反応、27g～36gの間で炭酸水素ナトリウムと反応し、36gより多いところでは塩化水素が余っているとなります。よって(2)は➀が青色、➁が黄色となります。また、それぞれ反応する塩化水素の重さがわかったため、(3)と(4)は反応１、２を見れば簡単に計算できます。

(5) 水溶液Aの水酸化ナトリウムがすべて塩化水素と反応した地点を「点P」と呼ぶことにします。点Pは反応１が終わった時点であり、反応２が起こり始めた時点でもあり、さらに、炭酸水素ナトリウムがほぼ完全に残っている時点と考えることができます。次の文あ～おのうち、それぞれの文中の仮定が正しいとしたときの点Pの考察として適する文を２つ選びなさい。
あ　水溶液中に塩化水素が少しでも残っていたら刺激臭を感じることができると仮定すると、水溶液Aに塩酸を少しずつ加えていき、刺激臭を感じた時点が点Pといえる。
い　塩化ナトリウムが水に溶けないと仮定すると、水溶液Aに塩酸を少しずつ加えていき、白いにごり（溶け残り）が見られた時点が点Pといえる。
う　二酸化炭素が水に溶けないと仮定すると、水溶液Aに塩酸を少しずつ加えていき、気体の発生が見られた時点が点Pといえる。
え　溶けている物質は変化させずに、水酸化ナトリウム水溶液の色だけを赤色にすることができる薬品があると仮定すると、この薬品を加えた水溶液Aに塩酸を少しずつ加えていき、赤色が消えた時点が点Pといえる。
お　溶けている物質は変化させずに、炭酸水素ナトリウム水溶液の色だけを赤色にすることができる薬品があると仮定すると、この薬品を加えた水溶液Aに塩酸を少しずつ加えていき、赤色が消えた時点が点Pといえる。

仮定がユニークな問題ではありますが、あは塩酸が残る＝塩化水素36g以上なので✕、いは食塩が生じる＝少しでも塩酸を加えたときなので✕、うは二酸化炭素が発生し始めるのは反応２が起こり始めた時点なので〇、えは水酸化ナトリウムがなくなる＝反応１が終わるなので〇、おは炭酸水素ナトリウムがなくなる＝反応２が終わるなので✕、というように、実験の内容と、仮定で言おうとしていることを整理すれば簡単に選べます。結果の裏で何が起きているかを意識的に確認するくせをつけましょう。