私が指導の際に重視しているのは、次の3点です。

❶　解法や考え方に名前をつける
❷　最速の論理プロセスを構築する
❸　苦手分野とミスの傾向を可視化する

順にご説明いたします。

❶　解法や考え方に名前をつける
小6の2学期以降、多くの生徒が過去問演習に入ります。はじめは特に苦戦する子が多いです。
また、非受験学年でも「出題範囲の広いテスト」や「範囲のない模試」を苦手とするお子様が毎年います。
その主な原因のひとつは、「どの解法を使えばよいか」を正しく選べないことです。
そこで私は、解法や思考パターンに“名前”をつけて整理するよう指導しています。
これにより、次のようなメリットが生まれます。

• ぼんやりしていた解き方を忘れにくくなる
• どんな場面で使えばよいか明確になる　→　初見の問題に対する対応力が上がる
• 異なる単元間でも共通点を見出せるため、相乗効果が生まれる

▶例：【その他大勢、勝手に決まる】

問題
白のご石が4個、黒のご石が2個、合計6個のご石を一列に並べます。
並べ方は何通りあるでしょうか。

まず、6個のご石を入れる「箱」を用意します。

6か所のうち、黒いご石を置く2か所を選びます。
順序は関係ないので「組み合わせ」ですね。

6×5÷(2×1)＝15通りです。

黒のご石の位置が決まると、白のご石は自動的に残りの位置に入ります。
つまり、白については考えなくてもよいのです。
これが【その他大勢、勝手に決まる】型の問題です。
一方を決めることで、もう一方が自然に決まる。
この「依存関係を見抜く」発想は、応用問題を解く際の土台になります。

❷　最速の論理プロセスを構築する

首都圏の難関校では、思考力・論理力を問う問題の比重が高くなっています。
時間制限の中で「どのように考えを組み立て、どの順で整理していくか」が勝負です。
単に「正解にたどり着く」だけでなく、最短で矛盾なく結論を導くプロセスを作る力を鍛えます。
この点については、後述の「指導実例」で具体的にご紹介します。

❸　苦手分野とミスの傾向を可視化する

これは生徒本人にはほとんど見せませんが、各単元の理解度・進捗を一覧で管理しています。
以下は一例です。

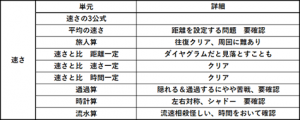
このデータをもとに、講習会や入試直前期の学習計画を組み立てています。

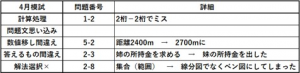
また、テストごとに「どんなミスをしたか」も記録。
必要に応じて本人にも共有し、自分のミスの傾向を把握する習慣を身につけさせます。
授業中の声かけや、扱う問題の選定にも、この記録を活用しています。
以下が一例です。

【筑駒中（2025年度）大問1より（一部表現変更）】
以下は、筑駒中の実際の入試問題をもとにした指導例です。
筑駒の入試は40分で4題を解くため、1題あたり約10分。
したがって「最速の論理プロセス構築」が極めて重要な学校です。

【問題】1から9までの整数のうち、いずれか1つが書かれたカードがあります。
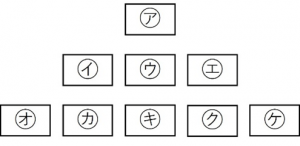
これらのカードを、下の図のようにならんだ㋐～㋘のマス目に1枚ずつ置くことを考えます。
ただし、㋐には1，2，3の3枚のカードから1枚を
㋑，㋒，㋓には4，4，5，5，6，6の6枚のカードから3枚を
㋔，㋕，㋖，㋗，㋘には7，7，7，8，8，8，9，9，9の9枚のカードから5枚を
それぞれ選んで置くものとします。
ここでは、たとえば㋐のマス目に置いたカードのことを、㋐のカードということにします。
次の問いに答えなさい。

(1)㋐，㋒，㋖のカードに書かれた3つの数について考えます。
㋐，㋒，㋖のカードに書かれた3つの数の合計が、3の倍数となりました。
このような3枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。

(2) ㋐，㋑，㋒，㋓，㋖のカードに書かれた5つの数について考えます。
㋐，㋒，㋖のカードに書かれた3つの数の合計と，㋑，㋒，㋓のカードに書かれた3つの数の合計が、どちらも3の倍数となりました。
このような5枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。

(3)㋐～㋘のカードに書かれた9つの数について考えます。
㋐，㋒，㋖のカードに書かれた3つの数の合計、
㋑，㋒，㋓のカードに書かれた3つの数の合計、
㋔，㋕，㋖，㋗，㋘のカードに書かれた5つの数の合計が、すべて3の倍数となりました。
このような9枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。

(1) まず、3の倍数条件の整理
1～9のカードを3で割った余りで分類します。
余り0 → 3、6、9
余り1 → 1、4、7
余り2 → 2、5、8

㋐と㋒が決まれば、㋖は自動的に決まることがわかります。

(例)　㋐が1，㋒が5ならば㋖は9

つまり、【その他大勢、勝手に決まる】型の問題ですね。
したがって、3×3＝9通りが答えです。

(2) 次に㋑と㋓を加えた場合
㋐，㋒，㋖が決まれば、残りは㋑と㋓。
このとき、数字の組み合わせは自動的に1通りに定まります。
※この事実に気付くスピード、差がつきそうですね。
㋑と㋓の並べ替えのみを考えればOK。
9×2＝18通りが答えです。

(3) 最後に全体（㋐～㋘）を考える
一見複雑に見えますが、考える順序の工夫で整理が可能です。
上から順に処理すると場合分けが増え、繁雑になりそうです。

※さらっと書いていますが、非常に重要な視点です。
㋖が7のとき、㋔，㋕，㋗，㋘に使う数字の組み合わせが複数あります。8、9のときでも同様になるため、実際そこそこ手間がかかります。

下段（㋔～㋘）から先に考えていきます。

(0，0，0，1，2)　
(0，0，1，1，1)
(0，1，1，2，2)　
(0，0，2，2，2)　

の4種類が3の倍数になる組み合わせです。

(0，0，0，1，2)　→　20通り
(0，0，1，1，2) →　10通り
(0，1，1，2，2)　→　30通り
(0，0，2，2，2)　→　10通り

並べ方の合計は70通り。

次に㋒を3通り選び、㋑と㋓の並べ替えが2通り。

最後に㋐は自動的に決まるため

70×3×2×1＝420通りが答えです。

ポイント

(1)(2)をスピーディに処理し、(3)を【その他大勢、勝手に決まる】型として「どこを先に考えるか」を戦略的に決めること。
これがこの問題の重要なポイントでした。

最後に

(3)のような思考力問題で論理を組み立てるには、以下の2つの要素が欠かせません。

● 生徒本人が失敗を恐れず、試行錯誤できる環境
● 間違っていても、その思考プロセスを正しく評価できる大人の存在

この2つを両立できるのが、個別指導の最大の強みです。

難問に対しても、試行錯誤しながら論理を組み立てる。そしてその過程を楽しむことを意識した指導を行ってまいります。