入試において安定して得点するためのカギを握る「平面図形」の解き方を、入試問題を例に説明いたします。

問題
鷗友学園女子中学校2024年（第一回）
図のような台形ABCDがあります。
BE：EF：FG：GC＝2：1：2：3です。また、AGとDCは平行です。

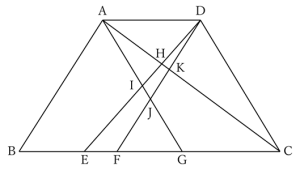
(1) AH：HK：KCを、最も簡単な整数の比で表しなさい。
(2) 台形ABCDの面積が15㎠のとき、四角形HIJKの面積を求めなさい。

平面図形の問題で重要なことは、与えられた条件から図形の特徴を正しく読み取ることです。また、その特徴を生かして解くために必要な知識を事前に確認し、利用するトレーニングを積み、テクニックを磨いておくことです。

今回は、台形がベースになっており、その中に直線を書くことで相似な図形が生まれているので、その特徴を活用して問題を解いていきましょう。

まず、AGとDCは平行なので、四角形AGCDは２組の対辺がそれぞれ平行です。四角形AGCDが平行四辺形であることに注目しましょう。平行四辺形の対辺は等しいので、AD＝GCとなります。

このような気づきも知識を利用するトレーニングをきちんと繰り返すことで生まれます。学習にはいくつか段階があり、知識を得たからすぐに使えるようになるわけではありません。基本的な動作を当たり前にできるように、的確な練習を行うことは大切です。

(1)の問いでは、辺ACが点Hや点Kによってどのような長さに区切られるか問われています。そこで、点Hや点Kがどのような位置にある点なのか考えて見ましょう。
このとき、線が沢山重なって視界に入ると目移りしてしまい考えがまとまらないようであれば、点Hの位置を決めるのに必要な線だけ書いてみると分かりやすくなります。


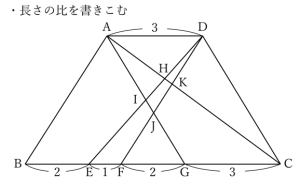
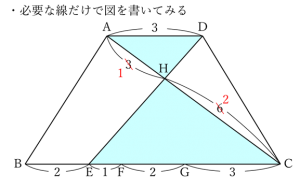
テストには制限時間があるので、最終的には与えられた図形の中に情報を整理して解けることが理想的です。そのような力を身につけるための練習を行っている段階では丁寧に取り組むことも効果的です。情報量の多さに応じた整理を行えるように練習しましょう。

点Hによって辺ACはAH：HC＝1:2に区切られることが分かりました。
同じように考えると、点Kによって辺ACはAK：KC＝3:5に区切られることも分かります。

それでは、AH：HK：KCを求めていきましょう。
辺の長さが２点で３か所に区切られるときに長さの比を問われる機会は非常に多いので、自分なりの「整理の型」を決めておくとスムーズに処理が進みます。
例えば、次の図のように書き出しても良いですし、式の形でまとめても構いません。
自分自身が素早く正確に処理できる方法を選びましょう。


これでAH：HK：KC＝8：1：15であることが分かりました。

次に(2)の問いについてです。
台形ABCDの面積が15㎠と条件が与えられたので、ここから四角形HIJKの面積につなげていくことを考えます。

ここで注目したいのは、(1)で点Hと点Kによって辺ACがどのように区切られるか既に求めていることです。このことを生かせるような方向性で考えましょう。
図形をいくつかに区切ると辺の長さによって面積が決まります。
今回は、台形ABCD→三角形AGC→三角形AJKと区切っていき、最後は三角形AJKから三角形AIHの面積を取り除くという流れで解いてみましょう。

まずは、台形ABCDの上底と下底の和に対して、三角形AGCがどのくらいの長さを占めているかに着目します。台形ABCDの面積の何倍の面積になるか、割合でとらえていきましょう。

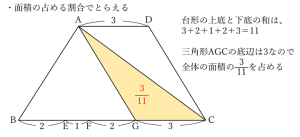
さらに、三角形AJKと三角形AIHの割合も求めます。
点Iや点Jの位置は、(1)と同様に相似な図形に着目して考えましょう。
AI：IJ：JG＝5：1：4と分かります。


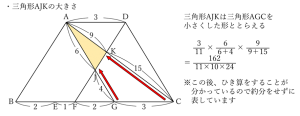
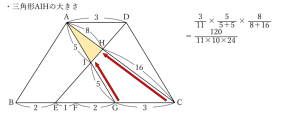
最後にこの２つの三角形の差から、四角形HIJKの割合を求めて解答をまとめましょう。

問題集を用いた単元の学習ではなかなか出てこないような数値ですが、今回の問題ではこれが解答です。扱われる数値の複雑さは受験する学校によっても異なるので、必要に応じた計算力も算数の基礎的な力として磨きをかけていきましょう。

特に平面図形の問題は、複雑な見た目をしているだけで必要以上に難しく考えてしまいがちです。きちんと基礎的な事から理解していることを確認し、どのように利用すればよいのかが分かれば、一見難しそうに見える問題も的確に解くことができます。

指導の際には、生徒毎にどこまで理解できていて、どこからつまずきがあり解答できないのかが異なります。そのつまずきを取り除きながら「自分の力で問題が解ける」という状態に導くことに力を入れております。