最初の一歩を踏み出す

最初の一歩を踏み出しなさい。途中の階段の全てを見る必要はない。
キング牧師の言葉です。

算数の得意、不得意を決定づける最大の要素は何でしょうか？私は、問題の解き始めに、最初の一歩を自分で踏み出せるかどうかだと考えています。
問題を読み、分からない！となったときに、まず何をするのか。式にしてみるのか、図や表で整理するのか・・・
この「最初の一歩」が最も大切で、最も難しいのです。

世田谷学園中学平成28年度第一次試験の問題（改題）を例に見ていきましょう。
数式などは出てきませんので、お気軽にお読みください。

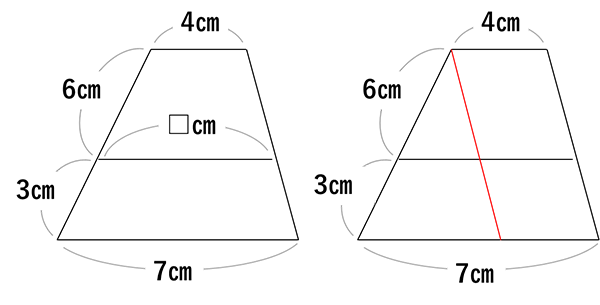
平面図形の問題です。この形の類題は多くのテキスト・問題集に収録されており、それら掲載されている模範解答は、上の右の図のように、斜辺と平行な補助線を引いて解く、とされています。
しかし、この問題を見た際に「そうか、この形は平行な補助線を引くのか」と覚えるだけの勉強をしているようでは、残念ながら成績の伸びは期待できません。
この問題で身に着けるべき事柄は、もっと根本に基づいたものなのです。
平面図形の相似で最も多く出題される形は、下の二種類です。
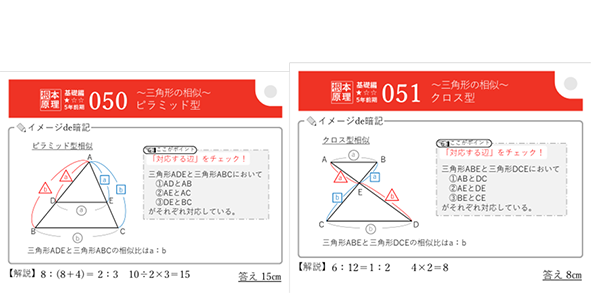平面図形の相似問題とは、問題の図の中から、上の二つの形を「探す」ことが最初の一歩です。
さて、改めて例題を見ると、どこにもクロス型もピラミッド型も見つかりません。
ですから・・・ないならば作ればいい！　この発想が補助線の原点です。
つまり、意識としては「平行線を引こう」ではなく
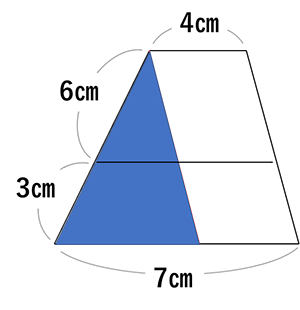「ピラミッド型の相似を作りたい」という気持ちが先にあり、その手段として、上の図の位置に補助線を引くことを思いつくのです。
ピラミッドの形を作ることが目的ですので、下の5本のどの補助線を引いても、問題を解くことが出来ます。
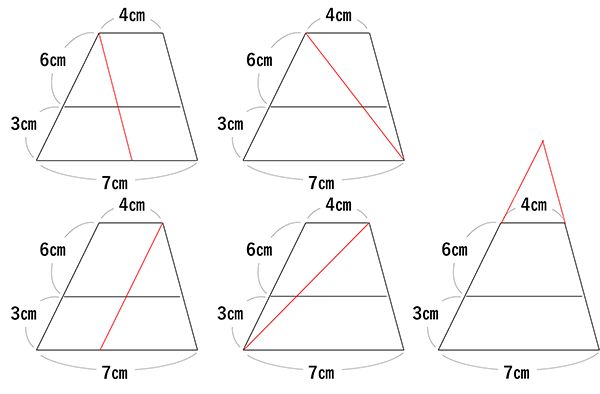同じ問題に取り組んでいても、指導者の目的意識の違いによって、丸暗記に頼るのか、根本の理解を目指すのか、結果が大きく変わります。
「この問題はここに補助線を引くよ」のような指導はなるべくしないようにしています。
そうではなく「どこかに線を引いて、ピラミッドを作れないだろうか？」と問いかける形で指導しています。
すると、生徒が自分で考えるようになります。
このような指導を続けていくと、問題に取り組む際の目の色が変わっていくのが分かります。
始めの頃は、ただ覚えた知識を思い出そうとしていた子が、段々と自分の頭で考えるようになるのです。
教えてもらった知識を覚えるばかりを勉強だと思うのか。自ら考えて気づくことを勉強だと思うのか。この差は大きいです。
「へー」と「あー！」の間には大きな違いがあります。
「へー」は数日で忘れますが「あー！」は忘れません。自分で発見したことは、強く記憶に残ります。
教えすぎることで、生徒が考えるチャンスを奪ってはなりません。
講師がするべきことは、自力で気づけるように導くことです。
気づきの扉を開けるのは生徒自身です。私はその扉の前まで連れていきます。
そのためには何が必要なのでしょうか。私は「抽象的なものの具体化」と「指導者による生徒の読み取り」の二つが不可欠だと考えています。

１　数という抽象的なものの具体化

算数の問題の状況設定は、子供にとって、あまり身近なものではありません。
一定の速度で線上を動き続ける点P、川を上る途中でエンジンが壊れて流されるボート、水そうの底に空いた穴をふさがないまま水を注いで貯めようとする、など・・・
小学生は、まだ抽象的な事柄を扱うことが得意ではありません。
深く理解するためには、具体化という作業が必須となります。
問われている内容を、どこまで実体のあるモノとして捉えられるか。質感をもって身近に感じられるか。これが、生徒の興味を引き出し、理解力を倍増させるための鍵です。
実体化してイメージさせる力こそが、中学受験指導の講師に求められる解説力だと思います。
算数の世界と現実の世界を一つ一つ、つなげてあげるようにしていきます。
例えば「足の速い人と遅い人がどちらも100m走ったら、どちらが短い時間で到着する？」
と問いかければ、早い人だと答えてくれます。これが
「AさんとBさんの走る速さは3：2です。二人が同じ距離を進んだ時、二人のかかった時間の比は何：何ですか？」
という問題になると、2：3か3：2か迷ってしまうことがよくあります。こうした子への指導として、早い・遅いで単純化してイメージさせることが有効です。
つまり、早い人の方が短い時間で着くのだから、Aが2でBが3。時間の比は2：3だよ！　のようにイメージさせます。
すると、今までは「時間の比は速さの比の逆比」と呪文のように暗記していた状態から脱し、頭の中で二人の人間が走り出す映像が浮かぶようになります。
これが「具体化」です。この段階に達すると、忘れることがなくなり、応用問題で使いこなせるようになります。具体化は、小学生を指導する上で絶対に必要な過程です。
その子の興味や知識の状態に合わせて、言葉を選んでイメージさせる会話力も、算数講師には必要です。

「この問題が分からない」となった時、全く何も分からないことは珍しいです。
必ず、分からない原因となるポイントがあります。
この原因の特定をしないまま通り一遍の解説を聞くと、子供は「分かった気」になります。分かった気だけなので、数日で忘れます。
本当に子供の学力を上げ、一人で出来るようにしてあげるためには、ピンポイントの原因特定が不可欠です。
私はこの原因特定のプロセスを「トレース」と呼んでいます。
講師が生徒の思考回路をトレース（なぞる）し、生徒の目線に乗り移ったように考えます。
間違えた答案であっても、子供は子供なりに論理的に考え、正解だと信じてその答えを書いたのです。ならば、生徒の辿った思考の道筋を再現することで、その論理のどこに誤りがあるのか、どこでつまずいているのかを見つけてあげることが出来るはずです。
そして「きみはこう考えたけれども、ここはこういう理由でバツになる。正しくはこう考えるよ」と示して初めて、心から納得し、使いこなせるようになります。
例えば下のような例題を見てください。

ＡＢＣの3人がいます。3人の身長の合計は335㎝です。Ａの身長はＢの1.2倍です。ＣはＢより15㎝高いです。3人の身長を求めなさい。

この問題を、生徒は解くことが出来ず、解答欄は空白でした。しかし、問題用紙には下のような図が描かれていました。（実際に6年生の生徒のテストの問題用紙に残されていた作図を再現しています。）
この図を見ると、線分図を描くというという最初の一歩まではたどり着いていることが分かります。そして、ＡＢＣの3人がいることと、合計の数値335㎝までは書けていますが、3人の線が描けていません。
正しい線分図は、下のようなものになります。
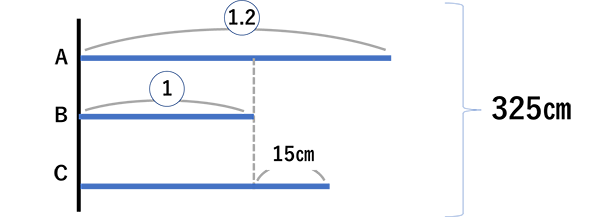しかし、この生徒に上の線分図を示し、こういう図を描いて解くのだ、と教えても、効果は薄いです。
なぜか？　その答えを探るために、もう少し深く考えていきましょう。
まず、なぜこの生徒は、途中で図が描けなくなってしまったのでしょうか。
普段の様子を見ていると、単純な和差算、線分図は理解しているはずなのです。
つまり、この問題が和差算であり、線分図を描くことまでは分かっていた。しかし、この問題特有の事情により、途中で図が描けなくなってしまった。 その原因は何か・・・？　と探偵のように考えていくと、少しずつ生徒の気持ちや考えが見えてきます。
実はこの問題は、ＡがＢより大きく、ＣもＢより大きいのですが、ＡとＣのどちらが大きいのか、解き始めの段階では分からないのです。つまり 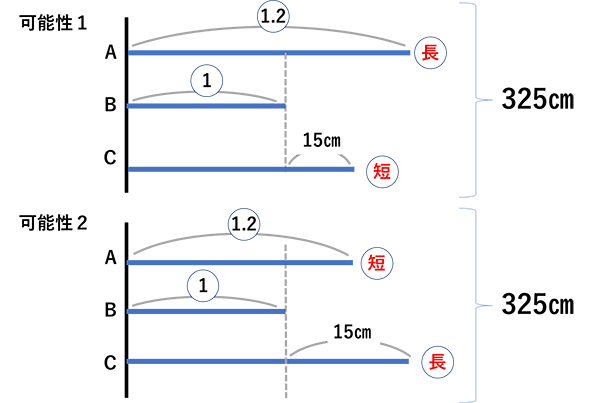上のどちらの図になるのか分からない。分からないから描けず、ここから先に進めなくなってしまっていたのです。
実際に生徒に聞いてみたところ、その通りだとのことでした。
つまり、この生徒に足りなかったのは「どちらの線が長いかは問題を解く上で関係なく、たとえ逆に描いてしまっても答えを出すことが出来る」ことを知らなかったという、ただこの一点なのです。
この場合、講師がやるべきことは通常の解説ではありません。「ＡとＣの長さは気にせず、適当に図を描いてみよう」という指導です。 わざとＣの方が長い図（可能性２の図）を描いて解き進め、最後の段階で、「あ、本当はＡの方が長かったんだ。でも問題を解くのには関係なかったね！」ということを体験してもらうのも良いでしょう。
このように、生徒の間違えたポイントによって、必要な解説や指導の量・種類は異なります。
講師がこれを正確に読み取れるかが、価値ある授業を提供できるかの差であり、そのための「トレース」なのです。
自分で気づき、最初の一歩を踏み出せる。具体的にイメージして考えられる。間違えたときにはピンポイントで指摘してもらえる。中学受験生には、こうした環境のそろった場所で勉強させてあげたいと思います。
自分で考え、力強く生きていける人間を育てることが、受験の目的です。真の問題解決力・思考力を、中学受験を通じて伸ばしていきましょう！

平成27年度、麻布中学の入学試験で出題された問題を例にとります。

以下の2つの条件に当てはまるような,3つの2桁の整数ア,イ,ウを求めなさい。
（条件1）アからウを引いた数とイからウを引いた数との比は2：7である。
（条件2）アにウを足した数とイにウを足した数との比は5：8である。

さて、この問題の第一歩は「とりあえず式か図にしてみる」です。

ア－ウ：イ－ウ
②：⑦
ア＋ウ：イ＋ウ
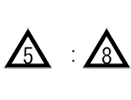さて、ここから何をすれば良いでしょうか。2種類の比がありますので、比をそろえることを目指します。
もしも生徒が、比を揃えるという「最初の一歩」を思いつかなかった場合には
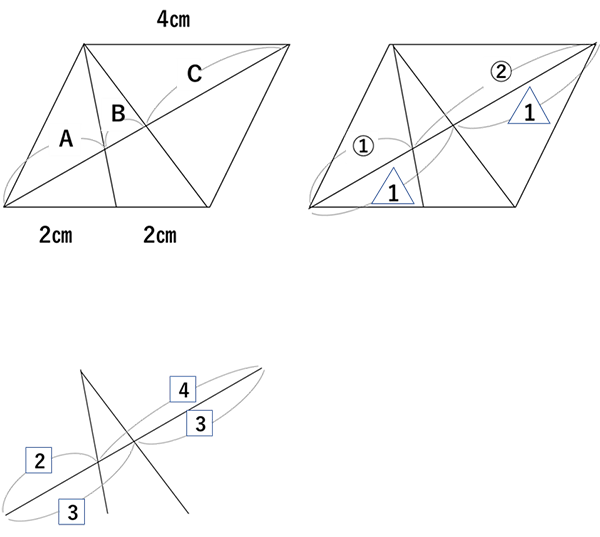こうした別単元の問題を出し、2種類の比がある時は比を揃えると良いことがある、という意識付けをしてあげます。
そうして準備してから改めて最初の問題を見せることで、比をそろえるという最初の一歩に気づいてもらいます。
このように気づきの扉の手前まで誘導し、自分で扉を開いてもらいます。
さて、今回の問題の場合はどうでしょうか。
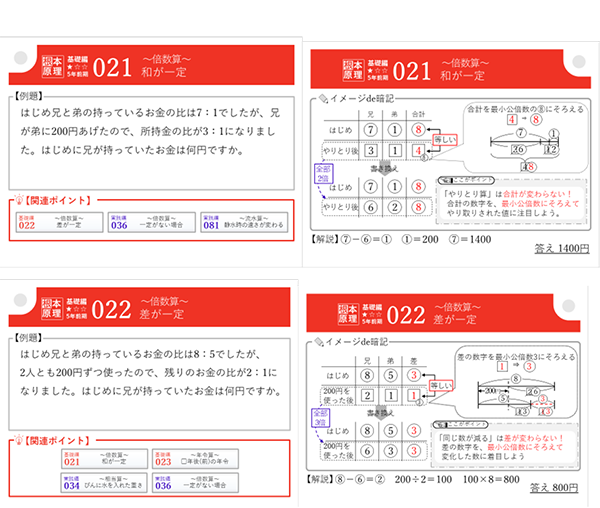
線分図で比を合わせるとなると、思い浮かぶ根本原理は「和が一定」（基礎編21）と「差が一定」（基礎編22）などが思い浮かびます。 それぞれ、以下のような問題です。
さて、本問を見ていきます。
アとイから、それぞれ同じもの（ウ）を引いた同士の比と、足した同士の比です。同じものを足したり引いたりしていますので、これは差が一定のパターンです。
これも、生徒が気づけない場合は身近な例で置き換えてみます。
例えば「私が今1000円持っていて、あなたは今1200円持っています。つまり二人の差は200円です。二人が500円ずつ使ったら、金額の差は変わるだろうか？」のように、抽象的な問題設定を具体的な日常世界に関連付けていきます。
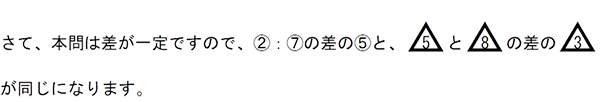この5と3を、最小公倍数の15に合わせます。すると
ア－ウ：イ－ウ
⑥：㉑
ア＋ウ：イ＋ウ
㉕：㊵
となります。
25－6＝19　（又は40－21＝19）
であるからといって、ウが19、としないように気を付けなければなりません。これは間違いです。
似た考え方としては、実践編68（速さ）があります。
二人が向かい合って進み、出会った場所が中間地点から100mの所だった場合、二人が歩いた距離の差は200mです。
これと同じように、6と25の差の19は、ウ二つ分です。よって、ウは9.5です。これにより
ア：イ：ウ＝15.5：30.5：9.5
となり、整数に直すと
ア：イ：ウ＝31：61：19
となるため、答えは（31,61,19）です。
いかがでしたでしょうか。
難関校の入試問題であっても
まず式にしてみる、という第一歩
差が一定などのポイントに自分で気づくこと
抽象的な数値をイメージするための具体化
手が止まった箇所では講師がその原因をピンポイントで読み取ること
解けるようになるために必要なことはシンプルであり、努力次第で習得することが出来ます。
必要な要素の詰まった勉強を十分な量積めば、成績は面白いように伸びていきます。
是非、こうした授業を体験してみてください。
「勉強」という言葉のイメージがひっくり返るかもしれません。
論理的に考える力を付けて成長するため、一緒に中学受験の勉強をしていきましょう！