特別編⑦ 2016 第25回算数オリンピックファイナル 問題解説(その4)
はじめに
受験Dr.の亀井章三です。いつも「開成・筑駒・灘中!すべて合格大作戦!」をお読みいただきありがとうございます。今回は、いつもの形式を離れた特別編!7月24日(日)に実施された「第25回算数オリンピックファイナル」の問題を1問ずつわかりやすく解説してまいります。
本連載では、いつも応用問題を解くために必要な「解法ポイント」というものをご紹介しています。今回のファイナル問題を解いていくうえでも、もちろんこの「解法ポイント」を使っていくことで簡単に解いていくことができますので、たくさん「解法ポイント」をご紹介してまいります。
【問題7】
1、2、3、4、・・・という数の列は、自然数(1以上の整数)の列と呼ばれます。ある数から始めて等しい数ずつ増える数の列を等差数列と呼びますが、1、2、3、4、・・・も、
1からはじまり1ずつ増える等差数列です。
この数列の1番目の1から順に何個かを足し合わせた数は三角数とよばれています。
下図のように、三角形に並べることができるからです。
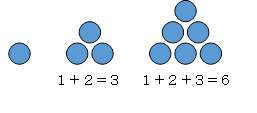
(1を1辺1個の三角形と考えて、以下、3は1辺2個の三角形、6は1辺3個の三角形、・・・・となります。)
三角数は、1、3、6、10、15、21、28、・・・と続きます。
ところで今年は2016年ですが、2016は63番目の三角数です。この2016に関連する等差数列について下の性質を持つようなものを考えます。
ある等差数列の1番目の数から順に何個かを足し合わせた数は、いずれも三角数になります。つまり、この数列のN番目を○Nとすると、
○1=三角数
○1+○2=三角数
○1+○2+○3=三角数
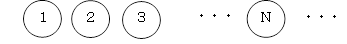
※以下同様に続く
このような性質を持つ(1以上の整数だけでできている)等差数列で、1番目の数から順に何個かを足し合わせることで2016が得られるものは、自然数の列を除いて全部で何通りありますか。ただし、始めの数字は1以外でよいものとします。
問題7は数の性質を利用した規則性に関する問題です。また、今年が西暦2016年であることから2016にちなんだ問題でもあります。いろいろな言葉が出てくるため、結局何について考えれば良いかが発想しにくい問題です。三角数をどう考えて表現していくかがポイントです。
<解説>
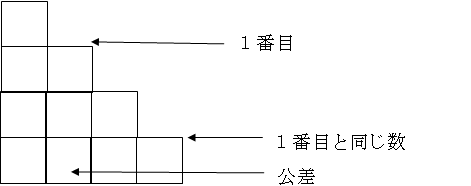
問題文のような正三角形ではなく、次の図のように「階段状の図形」で三角数を表現します。
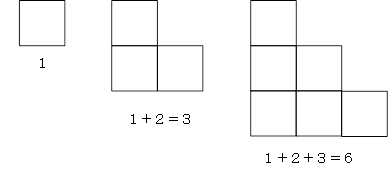
今回の問題のポイントは、等差数列の和が「常に三角数になる」という点です。つまり、1番目の数と公差に何らかの決まりが存在しないと、常に三角数にはならないわけです。その決まりを見つけることが解答につながります。
たとえば、1番目の数を3(=1+2)とします。
2番目の数は1番目の数+□(公差)ですから、次のように表すことができます。
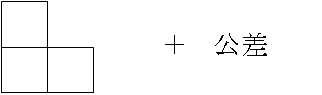
これがくっついても階段状の図形になるので、
となります。そうすると、3番目がくっついても

となり、常に三角数になります。
では、このような形で2016になるような数列はいくつあるのでしょうか。それは1番目の図形の段数に注目すればわかります。
1番目が2段のとき、2番目までくっつけると4段、3番目までくっつけると6段、と1番目の段数の倍数になります。
2016は63段の階段になりますので、「1番目の段数の倍数」が63になるものが条件を満たす数列です。
63の約数は1、3、7、9、21、63の6通りありますが、
1番目の段数が1段というのは自然数の列のことなので、それ以外の5つになります。
6+15+24+33+……+168+177+186=2016
28+77+126+175+224+273+322+371+420=2016
45+126+207+288+369+450+531=2016
231+672+1113=2016
2016は、その後5985、9954、13923……と続く数列の1番目です。
ではこれで全てでしょうか?
先ほどの例では、1番目の図形が2段でしたので、2段ずつ増える様子を考えました。これが3段ずつ増えるということはないか考えてみます。
図にしてみると
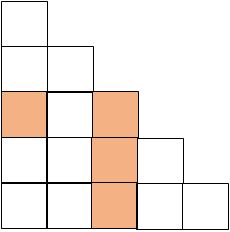
となります。
この場合3番目以降がくっついても常に階段状になります。
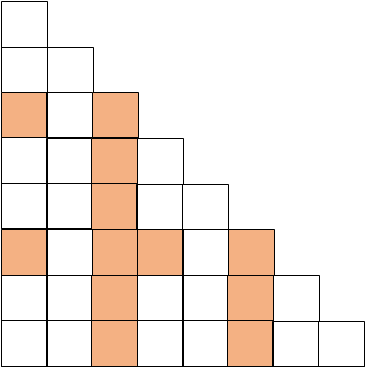
このことから、公差の部分が正方形にならないと条件を満たさないことがわかります。
では、このような形の数列を考えます。
1番目の図形の段数が□段のとき、(□+1)段ずつ増えていきます。この合計が63になる□(整数)を求めます。
□+(□+1)×○ =63
□+1+(□+1)×○=63+1=64
(□+1)×(○+1)=64
より、□は64の約数から1ひいた数になります。
64の約数は1、2、4、8、16、32、64の7個
ここから1をひくと、0、1、3、7、15、31、63
□は1以上の整数より、□=1、3、7、15、31、63となります。
□=1のときは自然数の列になるのでは?と思うかもしれません。しかし、公差が違うので別の数列になります。
1+5+9+13+……+113+117+121+125=2016
6+22+38+54+……+198+214+230+246=2016
28+92+156+220+284+348+412+476=2016
120+376+632+888=2016
496+1520=2016 (このあと、2544、3568…と続きます。)
2016はこのあと、6112、10208、14303…と続きます。
1番目の段数より2段以上多く増える場合は、公差の部分が正方形になりませんので、常に三角数になることはありません。したがって、答えは5+6=11通りとなります。
答え 11通り
規則や仕組みがわかりにくい問題こそ、とにかくやってみる、調べてみることが大切です。そして、その中から自分なりの仮説を立てることが真実を見つける方法です。頑張ってください。
【問題8】
立方体を、向かい合う3組の2面それぞれに平行な9個の平面、計27個の平面で切り、(10×10×10=)1000個の直方体に分けます。もとの立方体を保ったまま、切り口が立方体の頂点を結ぶ正三角形になるような平面で、この1000個の直方体の集まりをさらに切ったとき、切断された直方体は何個ありますか。最少の場合と最多の場合をそれぞれ求めなさい。
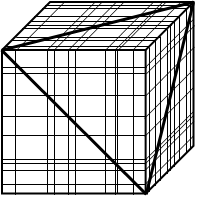
最後の問題8は、立体図形の切断に関する問題です。問題の設定自体はシンプルですが、27面で切るという数の多さから条件を考えていくのが難しい問題です。このような立体図形の問題を考えていくポイントをおぼえていきましょう。
<解説>
この問題のポイントは、1000個の立体に分けてから切断するのではなく、先に切断してから27個の面で分けていく、と順番を逆にして考える点
です。算数オリンピック2015トライアルの立体図形でも同じ方法が使える問題が出題されています。
どのように分けるかで、何個切断されるかを考えてみましょう。そこで、正三角形の部分だけ見えるように立体を描きます。
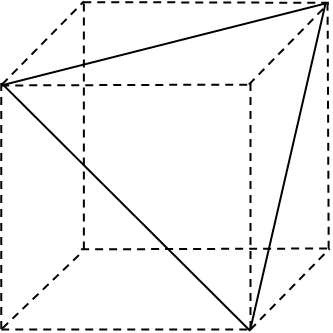
ここに平面を1つ交わらせると、
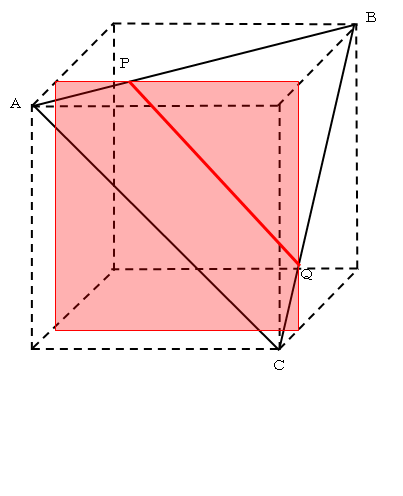
切り口(赤い面)は正三角形とPQで交わります。
立方体の面に平行に切ると、上の面、右の面、前の面の3面のうち必ず2面を切断するので、切り口は正三角形と必ず2点で交わり、交線を作ることになります。これは
【ポイント№24】「2つの交点、1つの交線」
のポイントを使っています。
その結果正三角形は2つの部分に分けられます。これは、赤い面で分けられた2つの直方体が、正三角形の切断面でどちらも切られていることと同じ意味です。
つまり、正三角形と平行面との交線により、正三角形がいくつの部分に分けられたかで、1000個のうち何個切断されるかがわかるわけです。
たとえば、

のようにすると、正三角形は3つに分けられ、
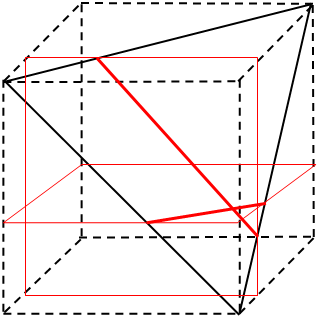
のようにすると、4つの部分にわけられます。
ということは、切断される長方形の個数が最少・最多になるのは、正三角形に辺と平行な直線を9×3=27本引き、できるだけ他の直線と交わらなかったときが最少、できるだけ他の直線と交わるようになったときが最多となります。
最少の場合を考えます。できるだけ交わらないのは、次のように切り分けたときです。

このとき、正三角形は9×3+1=28個の部分に分かれます。
次に最も多くなる場合を考えます。ある辺に平行に9本の線を引くと必ず10個の部分に分かれます。
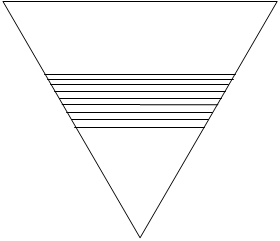
この9本の線全てに交わるように線を引くと
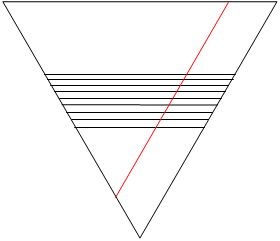
10個の部分が全て2つに分かれるので、全部で10×2=20個
になります。よって、9本引くことで
10×(9+1)=100個の部分に分かれます。
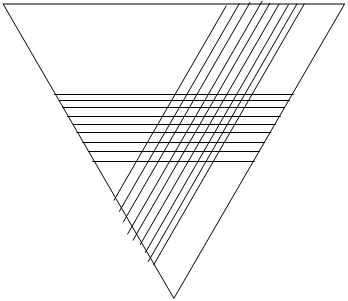
最後に残りの9本を引きます。
まず、1本の直線を既にひいた18本の線全てと交わるように引きます。
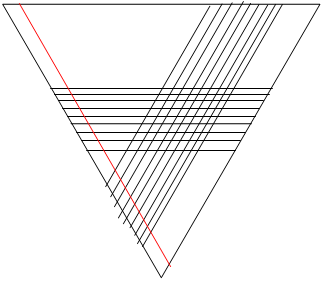
すると、1+8+1+8+1=19個の部分が2つに分けられ、全部で100+19=119個の部分になります。
つまり、18本全てと交わるように直線を引くと、18個の交点ができ、そのため19個の新たな部分ができるわけです。
したがって、全部で9本引くことで
100+19×9=271個の部分に分けられます。これが最多です。
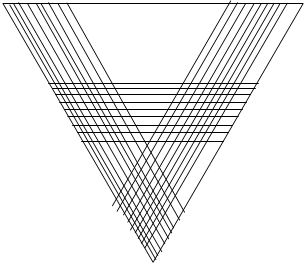
答え 最少28個 最多271個
以上で特別篇「2016算数オリンピックファイナル解説」は終了です。この文章を読まれて算数オリンピックに興味をもたれた小学5年生以下の方は、ぜひ来年トライアルにチャレンジされてはいかがでしょうか。そして、小学6年生の方は数学オリンピックにつながる「ジュニア広中杯」が待っていますので、そちらにチャレンジしてみましょう。

