特別編④ 2016 第25回算数オリンピックファイナル 問題解説(その1)
はじめに
受験Dr.の亀井章三です。いつも「開成・筑駒・灘中!すべて合格大作戦!」をお読みいただきありがとうございます。今回は、いつもの形式を離れた特別編!7月24日(日)に実施された「第25回算数オリンピックファイナル」の問題を1問ずつわかりやすく解説してまいります。
本連載では、いつも応用問題を解くために必要な「解法ポイント」というものをご紹介しています。今回のファイナル問題を解いていくうえでも、もちろんこの「解法ポイント」を使っていくことで簡単に解いていくことができますので、たくさん「解法ポイント」をご紹介してまいります。
【問題1】
3×3のマスがあります。この中に1~9の数字を1つずつ次の2つの規則に従うように入れていきます。
規則①:すべてのたてと横の列を考えると、3つの内で最も大きい数字は残りの2つの数字の和より大きく、その差はすべてのたてと横の列で同じ大きさである。
規則②:たての列の3つの数字の和は、右側の列が最大になるようにする。
図のマスの中に数字を入れて、完成させなさい。ただし、5はすでに入っています。
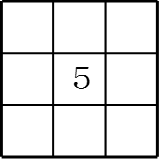
第1問は1~9を条件に合うようにマス目の中に入れる問題です。規則①をどう使っていくかがポイントです。
このように調べる個数が有限の場合、式だけで何とかしようとするよりも、効率よく調べ出すほうが確実に正解にたどりつけます。そこで次のポイントを使いましょう。
【ポイントNo.5】「計算する調べの作業は表で行う」
が使えます。
それでは解説です。
<解説>
規則①を2つの条件に分解します。
条件A「3つの数字の内で最も大きい数字は残りの2つの数字の和より大きい」
条件B「その差はすべてのたてと横の列で等しい」
条件Aを満たす3つの数の組合せを、条件Bで同じ差ずつ分類していきます。
このような場合、表にして一覧できるようにすると調べやすくなります。

たて、横3列ずつ計6列分の組み合わせがないといけませんので、差4~6はあり得ないことがわかります。
差が3の場合、1が入った組み合わせが4通りあります。
しかし、1は1つのマスにしか入れられず、列としてはたて、横1列ずつの計2列しか使えません。したがって、6通りを作ることはできません。
差が2の場合、1が入った組み合わせが5通りあります。この中から2通り選ぶとすると、残りの(9、5、2)(9、4、3)(8、4、2)(7、3、2)から4通り選ぶことになります。しかし、この中に2を使う組み合わせが3通りあるため、こちらも6通り全てを作ることはできません。
よって、6列全ての差は1で等しくなることがわかります。

このうち1を含むものが6通り。1を含まないものも6通りあります。そして、1を含むものから必ず2通り選びます。
1を含まないもののうち、2を含むものは4通り、2を含まないものが2通りあります。このうち2を含むものから必ず2通り選びますので、1も2も含まない(9、5、3)と(8、4、3)は6列の中に必ず入ることがわかります。
そうすると3は2回出てきましたので、残り4列の中に3が入るものはないことがわかります。まとめると、
(9、7、1)(8、6、1)(7、5、1)(6、4、1)
(4、2、1)から2つ
(9、6、2)(8、5、2)(7、4、2)から2つ選ぶことになります。
ここで、たての列に(9、5、3)という列がある、と仮定します。そうすると、
残りのたての列の中に9と5が入る列はありませんので、(7、4、2)と(8、6、1)が決まります。
横の列は(8、4、3)と仮定されますので、8と4を含まない列は、(9、6、2)(7、5、1)となります。
あとはこの仮定が正しいかどうかです。
9+5+3=17
7+4+2=13
8+6+1=15
となり、5を含む真ん中のたての列の和が一番大きくなるため、規則②に反しています。
よって仮定の「(9、5、3)はたて」という部分が誤りになり、「(9、5、3)は横の列」ということになります。
以上からマス目に入る数字の組み合わせも決まります。横の列の入り方が2通りありますので、答えは次の2通りどちらも正解になります。
答え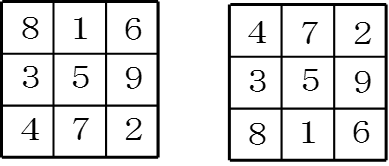
【問題2】
図のような1辺の長さが13cmの正六角形ABCDEFがあり、G、H、I、J、Kはそれぞれ辺AB、BC、CD、EF、FA上の点で、AG=BH=CI=EJ=FKです。
GIとHK、GJとKHの交わった点をそれぞれP、Qとします。PQの長さは何cmですか。
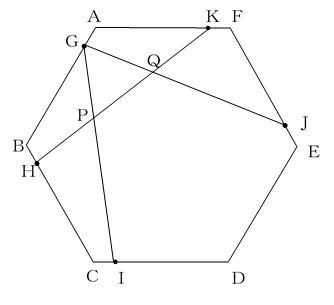
続いての第2問は、正六角形を用いた相似・面積の問題です。
PQの「長さ」を求めるために、どの辺の長さを求め、どの部分の比を求めるのか、作戦をしっかり立てていく必要があります。
<解説>
G、H、I、J、Kと正六角形の辺を同じ比で分ける点が打たれていますが、ただ1つ辺DEだけ点がありません。
図形の対称性を使うために、辺DEにもDG=2cmとなる点Lを打ちます。そして、HL、LK、IJも結んでみましょう。
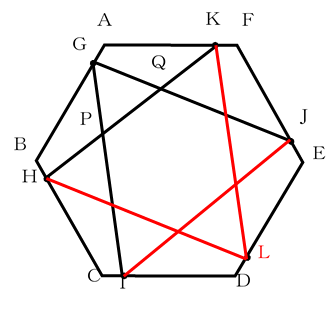
図形の対称性からKH=HL=LK=GI=IJ=JGとなるため、三角形KHLと三角形GIJは合同な正三角形になります。また、図形GHIJKLは正六角形になりますので、(なぜなら、三角形AGK、BHG,CIH、DLI、EJL、FKJはすべて合同なので)、
| PQはKHの | 1 | の長さになることがわかります。 |
| 3 |
あとはKHの長さがわかればOKです。
そこで、次の図のように正六角形の外側に正三角形を付け足します。
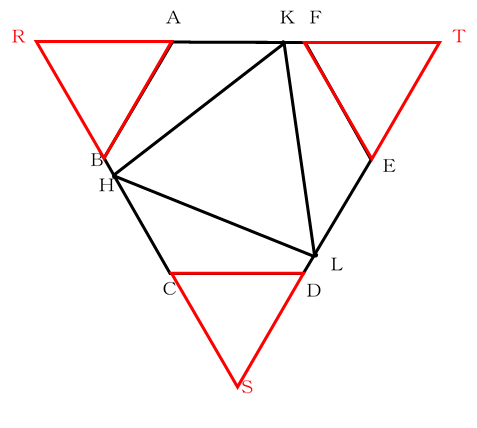
AB=AR=13cmより、三角形RSTは1辺39cmの正三角形になります。
また、AH=13+2=15cm、AK=13+11=24cmより、
三角形AKHの面積は、三角形RSTの面積の
| 15 | × | 24 | = | 40 | 倍になります。 | |
| 39 | 39 | 169 |
そこで、三角形RSTの面積を169とおくと、三角形KHLの面積は、169-40×3=49となります。
三角形RSTと三角形KHLはともに正三角形で相似形です。
よって、面積比が169:49=13×13=7×7であるならば、辺の比は13:7となります。
| したがって、KH=39× | 7 | =21cmとなり、 |
| 13 |
PQ=21÷3=7cmです。
答え 7cm
正六角形に辺が引かれているからといって、すぐに相似形を探したりしようとせず、問題の特殊な点に気づいていく感覚が大切です。
次回は問題3、問題4を説明いたします。

