第24回 図形の規則性を調べる
今後の目次
第24回 図形の規則性を調べる← 今週はココ!
今回は図形を用いた規則性の問題です。法則や作業はわかるのですが、数が大きくなったときにどうなるかが難しくなります。これは、「②解答にたどり着くまでの作業量が膨大で、効率良い解き方が見つかりにくく難しい。」という難しさです。
例に示された図を上手く使っていくことが重要です。今回は、このような図形の規則性の問題についてのポイントをご紹介いたします。
ポイントが身につく問題実践講座
問題
直角三角形を次のような操作で、いくつかの直角三角形に分割していきます。
ア.直角三角形の1つの辺を選び、その真ん中に印をつける。
イ.つけた印と直角三角形の頂点を線で結ぶ。
ウ.つけた印から直角三角形の他の辺に垂直な線をひく。ただし、選んだ辺が2つの直角三角形の辺になっているときには、その2つの三角形両方にイ、ウを行います。
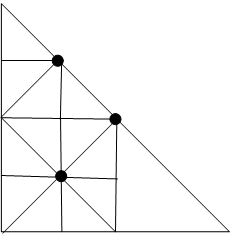
上の操作を1回とかぞえ、分割してできた直角三角形に、この操作を何回も繰り返して、下の図の直角三角形ABCを小さな直角三角形に分割していきます。
たとえば、1回目の操作を行うと、図1、図2のように4個、3個の直角三角形に分割されます。
また、2回目の操作を行うと、たとえば図3、図4のように8個、10個の直角三角形に分割されます。
さらに、3回目の操作を行うと、たとえば図5、図6のように10個、13個の直角三角形に分割されます。
次の問いに答えなさい。

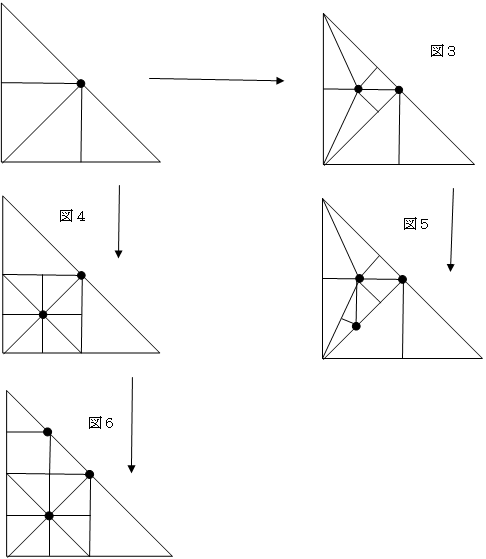
(1)操作を3回行ったとき、直角三角形ABCのそれぞれの辺に印が1つずつありました。直角三角形ABCは何個の直角三角形に分割されますか。考えられる個数をすべて答えなさい。
(2)操作を10回行ったとき、直角三角形ABCの辺上にある印は1個だけでした。直角三角形ABCは、最も多くて何個の直角三角形に分割されますか。また、最も少なくて何個の直角三角形に分割されますか。
(3)操作を50回行ったとき、辺AC上にある印は10個でした。直角三角形ABCは、最も多くて何個の直角三角形に分割されますか。また、最も少なくて何個の直角三角形に分割されますか。
(2005 筑波大付属駒場中 4)
【解くための考え方】
まずは、先ほどの問題を直接お子様に解かせてみてください。
どうでしたか?正解にたどりつけたでしょうか?
正解できなかった場合、どこまで解き進めることができたのかが重要です。(1)の作業を通して、何か規則性はみつけられたでしょうか。
今後受験Dr.では、「難問攻略イメージde暗記ポイント」カードを作成する予定です。
今回は、図形の規則性を考えていくためのポイントを2つご紹介します。
今回使うポイント
- 図形の規則性がとらえにくい
⇒【ポイント№14】「図形の規則は数字を並べて考える」
【ポイント№40】「規則性は例や前の問題の答えを利用」
【ポイント№14】「図形の規則は数字を並べて考える」
図形を用いた規則性の問題でも、問われているものは数字(個数・○番目)です。したがって、変化の規則を数字で示すことで問題を解くことができます。
この考え方は難関校に限らず、全ての学校で出題される問題に対しても必要なものです。そして、数字は表などに並べて記すようにしましょう。その方が、規則がわかりやすくなります。
今回は、点を打つ場所によって、三角形が何個増えるのか、まさに「変化の部分」をしっかりと数字でとらえていくことが攻略のポイントです。
(1)問題文の例にある図1、図2で、辺ACと辺ABに最初の点を打った場合の図が描かれています。
直角三角形は線対称な図形ですから、辺BCに最初の点を打つ場合は、図2と同じことになりますので省略します。
それぞれの図から、2つ目・3つ目の点を打つ図を考えましょう。
まずは図1から続ける場合です。
辺ABで点を打てる場所はアかイ、辺BCで点を打てる場所はウかエのどちらかになります。
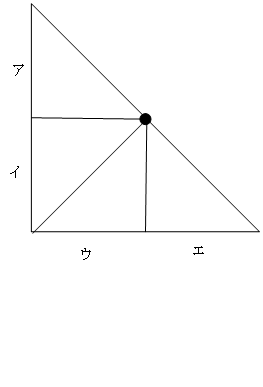
そして、ア~エのどこに打つとしても、それは図2のように、直角三角形の垂直な辺に点を打つことと同じ分け方になる、ということになります。
どこに点を打っても1つの三角形が3つの三角形に分かれますので、2つ増えることになります。
また、辺ABに打つことと辺BCに打つことは重複せず、線が交わったりしませんので、それぞれ独立して三角形を増やします。
よって、どこに打っても三角形の個数は4+2+2=8個になります。
次に図2から続ける場合です。

辺BCに打つときは1通り、辺ACに打つときは2通り考えられます。
図のオ~キのどこに打っても三角形は2つ増えます。
また、それぞれ独立しており重複することはありませんので、どの場所に点を打っても、三角形は3+2+2=7個になります。
これが考えられる個数の全てになります。
【ポイント№40】「規則性は例や前の問題の答えを利用」
(2)操作を10回行って、ABCの辺上に点が1個だけの場合です。
これは、最初の1個目だけ辺上に打ち、残りの9個は辺上にない場所に打つことになります。
そこで、どのような場所に点を打つと何個増えるのかを示された図を見て考えましょう。
図3や図4では、2つの三角形に共通する辺に点を打っています。
その場合は、問題文にもあるように2つの三角形に対して線を引きますので、増える三角形の個数も2倍になります。
そして、図3のように「垂直に交わる辺に点を打つ場合」は2つ増え、図4のように「斜辺に点を打つ場合」は3つ増えることもわかります。
このことから最も多い場合と最も少ない場合を考えます。
まずは、最も多い場合です。
多くする点の打ち方は、
・直角三角形の斜辺に打つ
・2つの三角形に共通する辺に打つ
ことになります。
そこで、例に示された図で使いやすいものはないか見てみましょう。
今示した条件を満たすのが図4です。
このあと、次のように点を打っていくと常に3×2=6個ずつ増えていきます。

したがって、4+6×(10-1)=58個が最も多い個数です。
最も少ない場合はどうでしょう。打ち方の条件は、
・直角三角形の垂直な辺に打つ
・2つの三角形に共通しない辺に打つ
となります。
最初の1個目の打ち方は辺AB(辺BC)となり、図1になります。
このとき、次の2個目をABCの辺以外に打つとすると、どうしても2つの三角形に共通の辺に打つことになります。
これは仕方ないので、次に「共通しない辺ができる」ように打ちましょう。そうすると下の図のようになります。
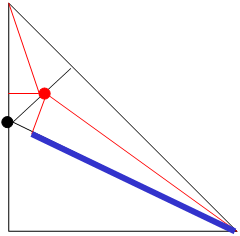
2個目は、ABCの内側の直線のうち、直角三角形の斜辺ではない方に打ちます。そうすると、青色の太線の部分が「2つの三角形に共通ではない辺」となります。あとは、この部分に点を打っていけば、2個ずつ増えていくだけになります。
よって、最も少ない個数は、
3+(2×2)+2×(10-2)=23個となります。
どんどん書いていって調べるのはもちろんOKですが、例で示されている図や、前の設問で描いた図を使い、時間短縮をはかりましょう。
それを意図して作問者も例を決めているわけです。
(3)最後は、(2)の応用です。
最も多い場合から考えます。
最初の点は斜辺である辺ACに打ちます(図1)。
ABCの辺に打つ残り9個の点も同様に辺ACに打っていきます。
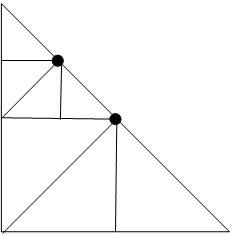
そうすると辺に点を打つたびに、3個ずつ三角形が増えます。
辺に打たない40個の点については、2つの直角三角形に共通している斜辺に打っていきます。
よって、個数は4+(10-1)×3+(50-10)×6=271個
となります。
最も少ない場合はどうでしょう。
まず最初の点は辺ABに打ちます(図2)
次に辺ACに点を打ちます。
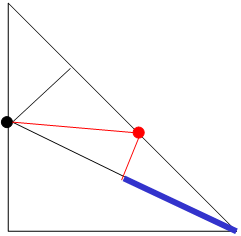
そうすると、増える三角形の数も最少の2個で済みますし、同時に「2つの三角形に共通でない辺(青色太線)」も作ることができます。
よって、個数は3+(10-1)×2+(50-10)×2=101個となります。
規則性は思考力だけでなく、問題文の読解力、応用力を試すことができ、入試問題では確実に出題される単元といえるでしょう。しっかり解法を身につけておきましょう。
【正解】
【正解】
(1)7個、8個
(2)最も多い 58個
最も少ない 23個
(3)最も多い 271個
最も少ない 101個
ポイントを使って開成・筑駒・灘の問題を解こう!
問題
円の周上にある偶数個の点を、次の<きまり>にしたがって、2つずつ選んでまっすぐな線で結びます。
<きまり>
・円の周上にあるどの点も、必ず1回だけ選びます。
・円の中にあるどの線も、交わらないようにします。
たとえば、円の周上に①から④の4個の点があるとき、このような線の引き方は、右の図の2通りです。
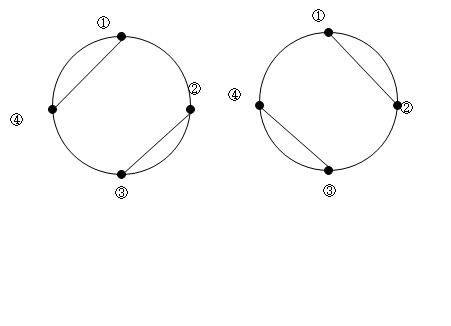
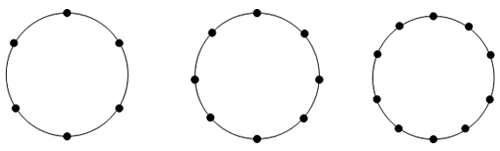
円の周上に次のように点があるとき、線の引き方はそれぞれ何通りありますか。
(1)①から⑥の6個の点があるとき
(2)①から⑧の8個の点があるとき
(3)①から⑩の10個の点があるとき
(2013 筑波大附属駒場中 3)
【解説】
(1)円周上に点がN個あるときの線の引き方をA(N)と表す
ことにします。A(2)=1、A(4)=2です。 ←ポイント№14
点が6つのとき、まず①をどの点を結ぶかを考え、場合分けします。
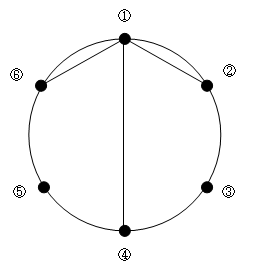
上の図のように、②、④、⑥と引くことができます。
③、⑤を結ぶと、線と線が交わってしまいます。
①と②を結んだとき、残り③~⑥の4つの点に、きまりにしたがって2本の直線を結びますが、これはA(4)と同じことになります。
よって、この場合は2通りあります。
①と④を結んだとき、線の左右に2個ずつの頂点が分かれます。
それぞれの結び方はA(2)=1通りなので、
1×1=1通りです。
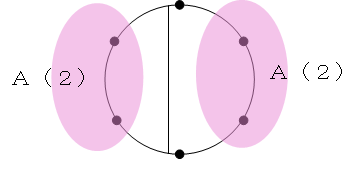
①と⑥を結んだときは、残り②~⑤の4つの点に2本の直線を引きますので、こちらもA(4)=2通りとなります。
したがって、A(6)=2×2+1×1=5通りです。
答え:(1)5通り
(2)
(1)から、最初の1本目を引くことで、残りの頂点の引き方が計算で求められます。 ←ポイント№40
8個の点がある場合も、①から時計まわりに②~⑧と番号を振って考えると、
①と②を結ぶ⇒A(6)=5通り
①と④を結ぶ⇒②と③を結び、⑤~⑧の4個を2本の直線で結ぶ
=A(2)×A(4)=2通り
①と⑥を結ぶ⇒①と④を結ぶときと同じ、2通り
①と⑧を結ぶ⇒①と②を結ぶときと同じ、5通り
したがって、5+2+2+5=14通りとなります。
答え:(2)14通り
(3)
これも同様に考えられます。
①と②を結ぶ⇒A(8)=14通り
①と④を結ぶ⇒A(2)×A(6)=1×5=5通り
①と⑥を結ぶ⇒A(4)×A(4)=2×2=4通り
①と⑧を結ぶ⇒A(6)×A(2)=5×1=5通り
①と⑩を結ぶ⇒A(8)=14通り
したがって、14+5+4+5+14=42通りとなります。
答え:(3)42通り
前回のチャレンジ問題の答え
問題
AB=13㎝、BC=12㎝、CA=5㎝の直角三角形ABCがあります。円を直角三角形ABCの辺に沿って下の図のようにP1→
P2→P3→P1の順に動かします。
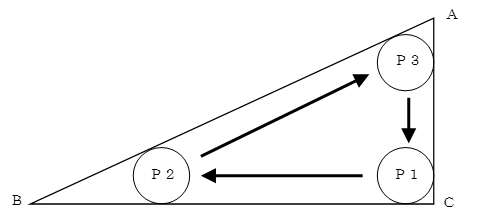
①半径1㎝の円を動かすとき、円が通過した部分の面積を求めなさい。

②半径0.5㎝の円を動かすとき、円が通過した部分の面積を求めなさい。
(2012 駒場東邦中3(2))
【解説】
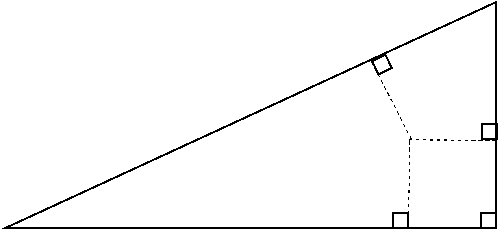
①円が動いた部分がわかるように図を描きます。
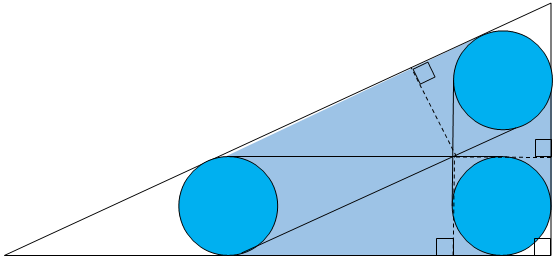
この円が動いた部分の面積は、三角形全体から白い部分を引いた値になります。
白い部分を近くに寄せると次のようになります。

三角形PQRは、三角形ABCと相似形で、相似比が2:1となります。
その理由ですが、三角形ABCに内接する円の半径を□cmとすると、
(13+12+5)×□÷2=12×5÷2
が成り立ち、□=2となるからです。
これはヘロンの公式と言って、中学校・高校の数学でも学習します。
したがって面積は、
12×5÷2-(30÷4-1×1×3.14)
=30-(7.5-3.14)
=30-4.36
=25.64
と求まります。
答え:① 25.64㎠
②円が動いた部分がわかるように図を描きます。
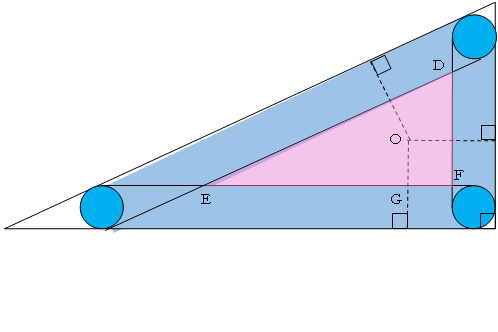
円が通らない部分は、白い部分と中央の直角三角形DEFです。
ここで、OG=1cmより、三角形DEFは①で考えた三角形PQRと
同じ形であることがわかります。
また、白い部分を寄せた形は、三角形PQRの1辺をさらに半分にした
直角三角形から、半径0.5cmの円を引いた部分になります。
したがって面積は、
30÷4÷4-0.5×0.5×3.14=1.875-0.785=1.09
30-(30÷4+1.09)=30-8.59=21.41
となります。
答え:② 21.41㎠
ポイントが確認できるチャレンジ問題
問題
1辺の長さが1cmの立方体を、たて・横・高さともに5個ずつ並ぶように机の上に積み上げる。3つ以上の面が見えている立方体を取り除くことにする。
1回目は右の図の赤色で示した4個を取り除く。
このような操作を何回か行うとき、次の問いに答えよ。
ただし、底面積は表面積に含めないことにする。
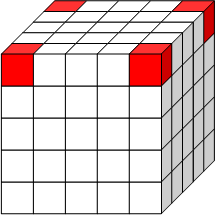
(1)2回目の操作の後、残った立体の体積と表面積を求めよ。
(2)3回目の操作の後、残った立体の体積と表面積を求めよ。
(3)全ての立方体が取り除かれるのは何回目の操作か求めよ。
(2001 灘中(二日目)2(改題))
※解答解説は次回掲載いたします。

