皆さま、こんにちは!
5月6日に「プレゼント交換」の問題について書きました。
次のような問題でしたね。
誰もが他人のプレゼントをもらうような交換の仕方は何通りありますか?
前回も書いたように、この問題を説明するのはけっこう大変なんです。
そこで、まずは次のような問題を考えてみてください、というところで前回は終わりました。
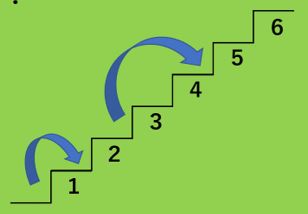
これは中学受験算数の入試ではとても有名な問題です。
受験ドクターの根本原理では、実践編246番のカードに出てきますよ!
では、さっそくこの問題の解説から今回は始めましょう。
「場合の数」を解くうえで、とても大切な考え方が出てきます。
それが何かを意識しながら、読んでみてください。
まず、この階段上りの問題を見て「あー、フィボナッチ数列でしょ!」と即答できる人はよく勉強しています。
お子様がすぐにわかるようでしたら、誉めてあげてくださいね!
フィボナッチ数列というのは、
1、1、2、3、5、8、13、21、34、55、89 …
というように、前の2つの数の和が次の数になる数列です。
先ほどの問題のような、「1歩で1段or 2段」で階段を上がる方法というのは、
1段の場合は1通り、2段の場合は2通り、3段の場合は3通り、4段の場合は5通り、5段の場合は8通り…
というようにフィボナッチ数列が答えとして現れます。
ですから、6段の場合の答えは、13通りが正解です。
ではなぜ、答えがフィボナッチ数列になるのでしょう?
それがきちんと説明できますか?
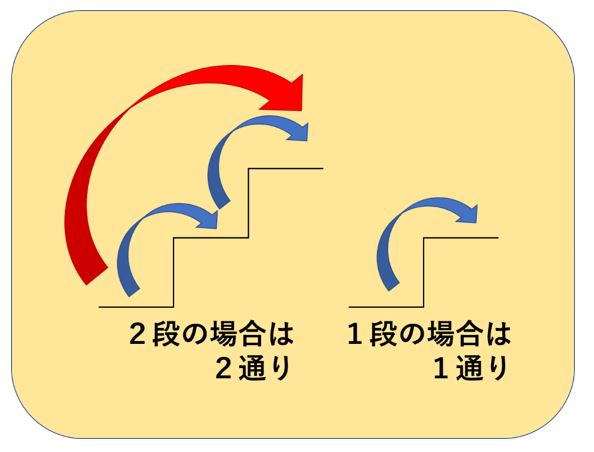
まず、階段が1段しかない場合と、2段しかない場合を考えてみましょう。
すると、次のようになります。
ここまでは簡単ですね。
問題は、3段のときをどう考えるかです。
地道に数えても3通りとわかるのですが、でもそれだと、もっと段数が増えたときに困ります。
そこで、次のように考えてみます。
わかりますか?
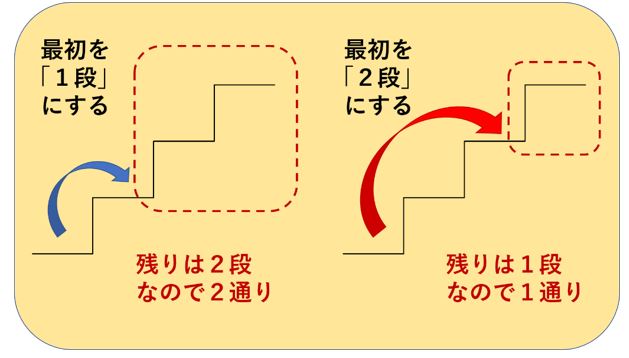
ポイントは、「最初の選択」で場合分けしていることです。
最初に「1段」を選択した場合は、残りは2段です。
最初に「2段」を選択した場合は、残りは1段です。
ですから、残り2段の2通りと、残り1段の1通りを足して、3段の上がり方は3通りと考えるのです。
これが理解できると、あとは何段になっても、これを続けていけばいいとわかります。
階段が4段あるなら、
最初に「1段」を選択した場合は、残りは3段で3通り
最初に「2段」を選択した場合は、残りは2段で2通り
と考えて、3+2=5通りです。
階段が5段あるなら、
最初に「1段」を選択した場合は、残りは4段で5通り
最初に「2段」を選択した場合は、残りは3段で3通り
と考えて、5+3=8通りです。
必ず直前の2つの答えを足して、次の答えが出てきます。
フィボナッチ数列ですよね?
わかってしまえばこれだけではあるのですが、ではこの問題のポイントはどこにあるでしょう?
それは、「場合分け」です。
「場合の数」の難しい問題では、適切に「場合分け」ができるかが勝負のカギを握ります。
「場合分け」をうまくできるかで、問題が簡単にも難しくもなりますね。
しかも、適切な「場合分け」というのが、必ずしも自分にとってわかりやすい「場合分け」とも限りません。
経験やセンスが必要な部分もあるので、ここが「場合の数」の学習で一番大変なところです。
見事な「場合分け」の仕方を色々と学んで、自分の中に取り入れていくことが大切になりますね。
階段上りの問題の場合は、最初の選択が「1段」か「2段」かで「場合分け」したのが素晴らしい発想でした。
さて、ではここからは、いよいよ「プレゼント交換」の問題を考えてみましょう。
先ほどの階段上りの問題と、いったいどんな関係があるでしょうか?
まず最初に、「プレゼント交換」を2人~7人で行った場合の答えを発表します。
答えは以下のようになります。
2人の場合→ 1通り
3人の場合→ 2通り
4人の場合→ 9通り
5人の場合→ 44通り
6人の場合→ 265通り
7人の場合→1854通り
4人の場合は、前回樹形図を書いて考えましたね。
そして、6人の場合の答えは265通りが正解です。
中学入試でも、この結果だけは覚えるように教えている塾もあるようですね。
しかし、人数が増えていくと、急激に数が増えて行きますね。
ではこの数字を見て、どんな規則性があるかわかりますか?
もしこの規則性を見抜けたら、数のセンスがかなり高い方です。
ヒントはフィボナッチ数列なのですが…
実はこの数列には次のような規則性があります。
4人の場合から順に行くと、
4人の場合→ ( 1+ 2)×3= 9
5人の場合→ ( 2+ 9)×4= 44
6人の場合→ ( 9+ 44)×5= 265
7人の場合→ (44+265)×6=1854
わかりますか?
フィボナッチ数列と同じで、前のかっこの中が直前の答えの2つの数の和になっていますね。
しかし、フィボナッチ数列と違うのは、その後に数をかけていることです。
しかも、その数は(人数-1)になっています。
これはいったいどういう意味なのでしょう?
さあ、ここからが「プレゼント交換」の問題の解説です。
ポイントは「場合分け」です!
しかも、今回は2段階で「場合分け」をするのです。
4人での「プレゼント交換」で考えてみましょう。
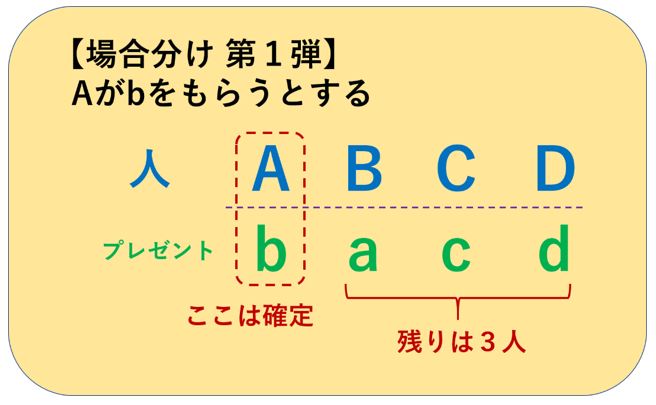
まず、A、B、C、Dの4人がいて、それぞれが持ってきたプレゼントがa、b、c、dとします。
そして、まずAがbをもらったとします。
これが「場合分け」の第1弾です。
すると、残りの状況は以下のようになりますね。
ここで「場合分け」の第2弾です!
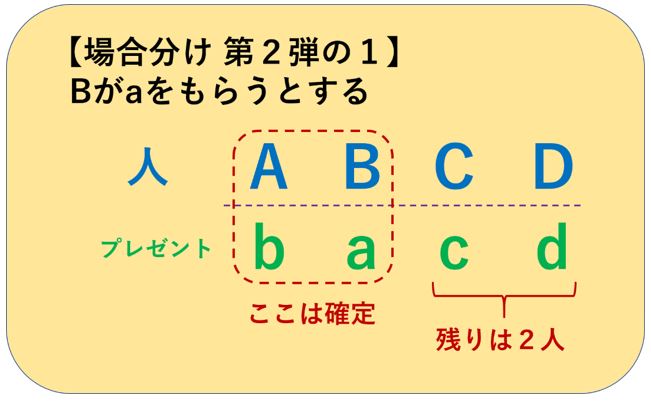
Bがaをもらうかもらわないか、でさらに「場合分け」するのです。
まず、Bがaをもらったとします。
すると、以下のようになりますね。
AとBの2人で交換したことになるので、あとはCとDで交換するしかありません。
ということは、Aがbをもらい、Bがaをもらわない場合は、2人で交換する場合の、1通りと同じです。
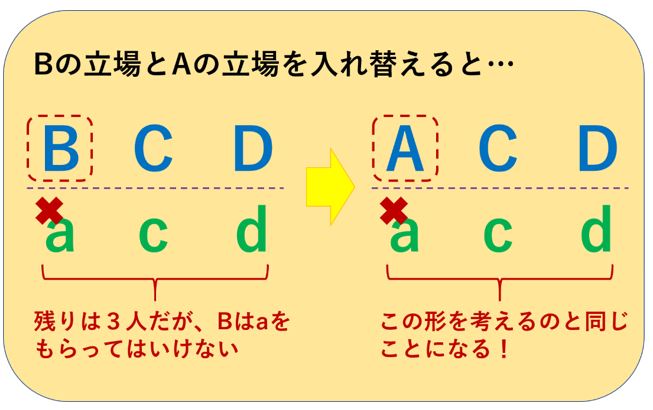
次に、Bがaをもらわない場合を考えます。
すると、状況としては3人で交換する場合と同じになります。
この意味がわかりますか?
ここがこの問題の最大のポイントです!
昔、初めてこの問題の解説を読んだとき、ここを理解するのに僕は1時間くらい考えました…
すぐに納得いかなくても大丈夫なので、落ち着いて考えてみてください。
Bがaをもらってはいけないと考えるなら、それはBの立場とAの立場を入れ替えることと同じです。
aとbのプレゼントの方を入れ替えると考えても良いです。
いずれにしても、3人で交換するのと同じことになります。
ですから、Aがbをもらい、Bがaをもらわない場合は、3人で交換する場合の2通りと同じなのです。
ここまでが理解できると、Aがbをもらう場合については、1通り+2通りで3通りになることがわかります。
ここが、フィボナッチ数列と同じ部分ですね。
そして、Aがcをもらう場合も、Aがdをもらう場合も、まったく同じように考えて、それぞれ3通りあります。
ここが、(人数-1)になる部分です。
Aがaをもらう場合はそもそも考えないので、その分が-1なのですね。
ですから、4人で「プレゼント交換」する場合の答えは、3通り×3通り=9通りと求まるのです。
わかりましたか?
これが理解できれば、5人の場合も同様です。
まず、Aがbをもらう場合を考えます。
そして、Bがaをもらう場合は、3人の場合と同じで2通り。
さらに、Bがaをもらわない場合は、4人の場合と同じで9通り。
よって、Aがbをもらう場合は、あわせて11通りです。
Aがcをもらう場合も、dをもらう場合も、eをもらう場合も、同様に11通りです。
ですので、11通り×4通りで44通りが答えになるのです。
6人なら、同様に考えて
(9+44)×5=265
となるので、答えは265通りになります。
いかがでしたか?
最後はちょっと難しかったでしょうか?
「プレゼント交換」の問題を公式化するなら、
(直前の2つの答えの和)×(人数-1)
となりますね。
高校数学なら、
という形で表現します。
もちろん、こんなことまで小学生が理解する必要はありません。
ただ、「場合の数」は中学でも高校でもやりますし、大学入試でも必須だということは知っておいてください。
ということで、今回は以上です。
難しいところもあったかもしれませんが、お伝えしたかったことは、「場合分け」の重要性です。
そして、「場合分け」がうまくなりたいなら、見事な「場合分け」の方法に触れてください、ということです。
「場合の数」は中学受験の算数でも重要分野です。
難関中学の入試問題では、高校生でも苦戦するような問題が出題されたりもします。
ぜひ、難しい問題でもあきらめずに取り組んでみてください!