皆さま、こんにちは！
５月になりましたね。
お子様たちも、そろそろ小学校の新学年・新クラスに慣れてきたでしょうか？
今年は長い長いゴールデンウィークなので、ここで勉強のペースを乱さないように気を付けたいですね。

さて、新学年や新クラスと言えば、気になるのは新しい座席！
仲の良い友達とか気になっている子とか、だれが隣になるかドキドキしたりしましたね。
新しい友達ができるチャンスだったりもしますしね。
思ったような席にならなくて「次の席替え早く来ーい」って念じているお子様も、すでにいるかもしれません。

そんな席替えのときに、自分の席の場所が前と変わらなくてガッカリしたことはないですか？
自分はそんなことなくても、周りのだれかがそういうことになっていたりとか。
ずいぶん運が悪いなーと思ったかもしれません。
でもこれ、実はけっこう高い確率で起こることなんです。
ご存知の方も多いかもしれませんが、クラスの人数が４０人くらいなら、およそ60％くらいの確率で起こり
ます。
しかも、不思議に感じるかもしれませんが、この確率は人数を増やしてもほとんど変わりません。
１００人でやろうが１０００人でやろうが、少なくとも１人が同じ席になってしまう確率は大体６０％なので
す。
詳しい解説は省略しますが、これは数学的に計算した明らかな事実なんです。

さて、席替えの話のように、並び替えた結果だれも同じ場所に戻らないような並び方を「撹乱順列」とか
「完全順列」と呼びます。
大学入試で時々扱われるテーマですね。
専門的にはモンモール問題と呼んだりしますが、一般的には「プレゼント交換の問題」として有名です。
次のような問題をちょっと考えてみてください。

さっきの席替えの話と同じで、自分のプレゼントが自分の手元に戻ってきたらがっかりですね。
できればみんなが、自分のプレゼントではないものをもらって帰りたいところです。
では、そんな交換の仕方は全部で何通りあるでしょうか？
一見すると、簡単そうな問題にも見えますね。
しかし、ちょっと考え出すとすぐに難問だということがわかります。
もし、この問題を完全な初見で解けたら、相当な算数力です。
自信のある方はぜひチャレンジしてみてください。

「答えと解説はないんかーい！」という声が聞こえてきそうです。
もちろんします！
でも、いきなりこの問題を解説するのはちょっと難しいので、段階を追って考えてみましょう。
まず、プレゼント交換に参加する人数が６人ではなくて、４人ならどうでしょう？
これなら、中学受験の問題でも見たことがあります。
樹形図を書いて、すべて書き出すことが可能なので、小学生でもなんとか解けます。
さっそくやってみましょう！

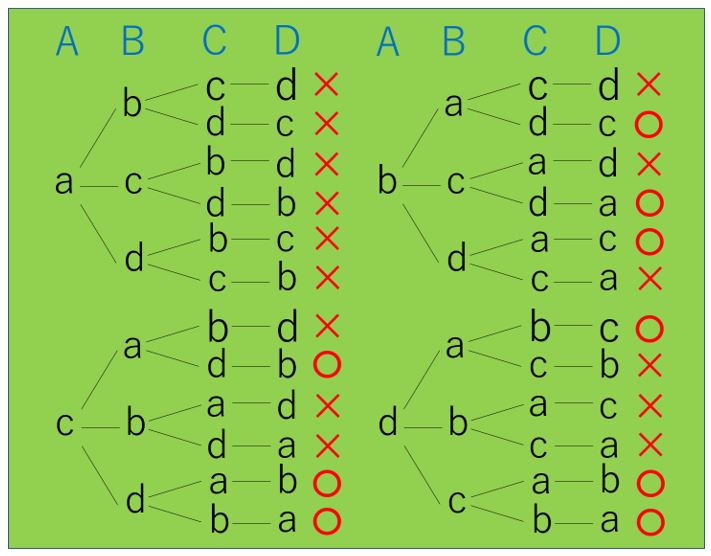
参加者はA、B、C、Dの４人だとします。
それぞれが持ってきたプレゼントはa、b、c、dとしましょう。
すると、それぞれのプレゼントのもらい方は、次のような樹形図で表されます。

どうでしょう？
４人それぞれが自分のものではないプレゼントをもらっているのは、９通りありますね？
ということで、これが正解です。
ちなみに、すべての交換の仕方は２４通りあります。
確率がわかる人ならば９÷２４✕１００で、３７．５%の確率で成功すると計算できますね。
逆に言えば、６２．５%の確率で、少なくともだれか一人は自分のプレゼントが手元に戻ってきてしまいます。
ランダムで交換すると、うまくいくのはけっこう難しいってことがわかりますね。
さあでは、これを６人でやるとどうでしょう？

ちょっと待って？
これを樹形図を書いて考えるってかなり大変じゃない？

そう思われた方の感覚は正しいです！
不可能ではないですが、かなり大変ですね。
コンピューターにでもやらせれば楽ですが、自分の手でやるのはちょっと躊躇します。
では、樹形図を書かずに何とか楽に求めることはできないでしょうか？
結論を先に書くと、できます！
実はとてもエレガントな求め方があって、それを知っていればわりと簡単に計算できます。
でも、そのエレガントな求め方をちゃんと理解するのは、けっこう大変なんです。
公式を覚えておくだけでいいなら、まあそれでもいいのですが、やっぱりちゃんと理解してだれかに説明
できるくらいになりたいですよね？
そんな方のために正しい解説をしたいのですが、そのまえに次の問題を考えてみてください。

これは中学入試ではとても有名な問題で、大概のテキストには載っています。
受験ドクターの根本原理では、実践編２４６番のカードに出てきます。
実はこの問題が、最初に書いた席替えやプレゼント交換の話と深いつながりがあるのです！
お子様がこれをさらっと解けたら、しっかりと勉強されているのは間違いないです。
たくさん褒めてあげてくださいね。
ということで、今回はここまでとします。

えー、ここでおしまい！？
という方は次回を楽しみにお待ちください。
せめて答えくらいは教えてよー、と感じる方は下の計算をしてみてください。
それぞれの計算の結果が、答えになります。
（ただし、それぞれの式は問題の解き方とは、直接の関係はありません）

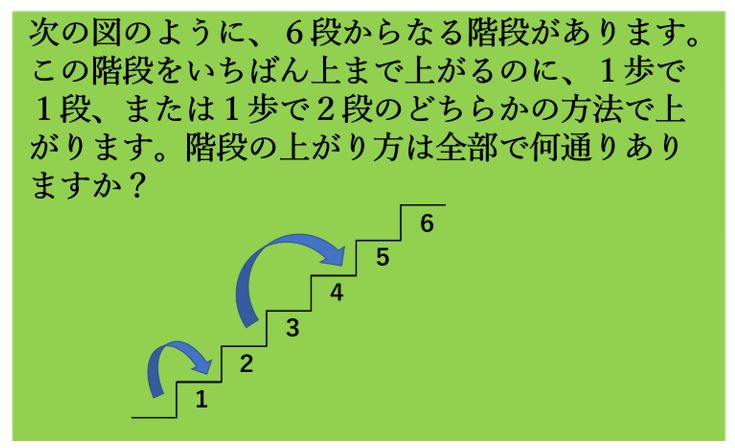
では、次回はこの階段上りの問題から解説します。
これがどうプレゼント交換の話とつながってくるかはお楽しみです。
興味のある方はぜひ考えてみてください。

それでは、またお会いしましょう！