こんにちは！RS講師です。
前回に引き続き、てこの難問を解くためのテクニックシリーズその②ということで、今回のテーマは重心です。

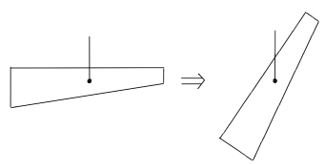
棒の重さが左右で異なる場合、棒は真ん中で支えても釣り合いません。
図のような場合、左側が太くて重たいために、棒は左へ傾きます。
このような棒を「太さが一様でない」と言います。

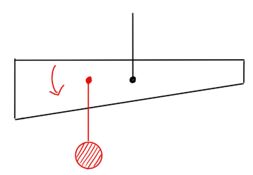
左に傾くのは、上のように目に見えないおもりが棒の左側にぶら下がっているからと考えることができます。

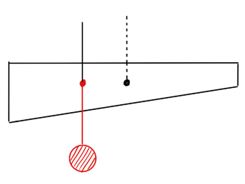
おもりの真上に糸をつるしてぶら下げると、赤いおもりに対して回転力は発生しないので、棒はどちらにも傾きません。
赤いおもりのある位置を、棒の「重心」と言います。

棒に重さがある問題では、このように重心の位置に、「架空のおもり（棒の重さぶん）」があると考えることで棒の重さをおもりに置き換えて考えていくのです。

さて、ここまではテキストに載っている基本の考え方です。
もう少し重心について理解を深めていきましょう。

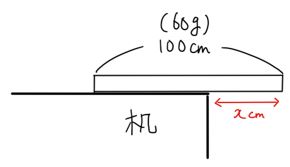
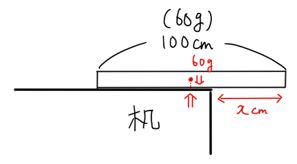
上の図のように、机のフチから均一な厚みの棒（100cm、60g）がはみ出ているとします。
この棒は、何cmまで落ちずにはみ出すことができるでしょうか？

これは、みなさん直感的に、「50cm」とわかると思います。なぜでしょうか？
原理について考えてみましょう。

まず、さきほどの話で、「棒の重心には、棒の重さと同じだけの重りがぶら下がっている」という考え方が出てきましたね。
その考え方に当てはめた時に、この棒は、下の図の赤い点の所に60gの力がかかっていることになります。したがって、この赤い点の真下に、机があれば赤い点は落ちずに支えられることになります。均一な棒なので赤い点は真ん中の位置（100÷2＝50cm）にあるので、x＝50cmとなるわけです。

＜複数の重心を考える＞
さて、上記の例を考えるにあたって、疑問に思うことはありませんか？
「実際には棒は、真ん中だけに物質があるわけではなく、全体に均一に広がっているんだから、支えている箇所は、赤い点の真下だけではないはずだ。なのに、なぜ赤い点だけを考えるの？」と。
子供達にはこういう疑問を大事にしてもらいたいですね。

はい。実際には、この疑問の通りです。
重心というのは、その物質が十分に硬くて変形しない時に（これを「剛体」といいます）、その物質の重さを代表して表している点をいいます。
なので、この棒全体を代表しているのは、ど真ん中の赤い点だけですが、次のように考えることもできます。

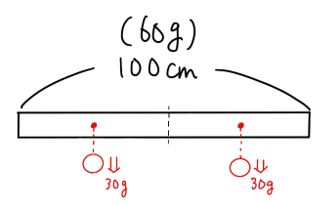
下の図のように、棒を2等分します。二つに分けられたので、左側は50㎝で30g、右側も50㎝で30gです。
分けられたそれぞれについて、その重さを代表する点（重心）を考えます。
日本を関東と、関西に分けてそれぞれの代表者を決めるような感じですね。

棒が机から一定量以上はみ出して右に傾く時、机の端（△）のところを支点にして、右回転が起こります。
ということは、棒が机から滑り落ちないギリギリの状態は、下の図のように、△を支点にして、左半分と、右半分の重心同士が釣り合っていると考えることもできるわけです。

これが、複雑な重心を考える際の手法になります。
一つやってみましょう。

【問題】
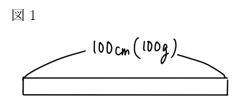
図1のような、均一な木材でできた長さ100cmの棒が何本かあります。
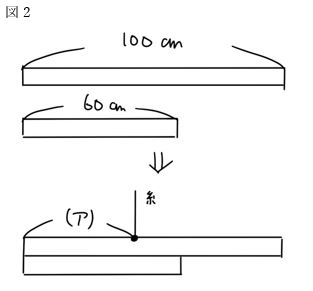
この棒を適当な長さに切り、重ね合わせて図2のようにボンドで固定しました。
この棒を一本の糸で支えて、左右どちらにも傾かないようにするには、（ア）の長さを何cmにすればよいでしょうか。

【考え方】
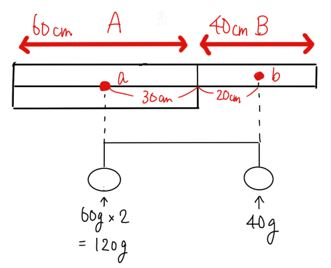
2枚重なっているところは、棒が重たくなりますので、2枚重なっているところをA、1枚のところをBと分けて考えてみましょう。

Aは60cm（60g）を2枚重ねたので120g、Bは40cmが1枚だから40gが、それぞれ重心の重さです。

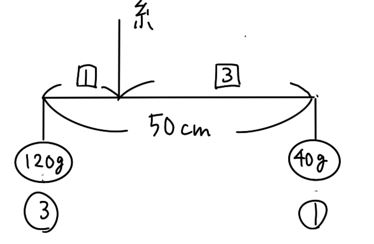
このように、50cmの棒の左に120g、右に40gぶら下がった状態と同じなので、
糸の位置は、左のおもりから、50×1/4＝12.5cmのところです。
したがって糸をぶら下げる位置、（ア）＝30＋12.5＝42.5cmとなります。

どうですか。コツさえ掴んでしまえばなんということは無いと思います。
このように重さが均一でない棒や、複数の板を貼り合わせたりする問題では、
均一な部分ごとにグループ化し、それぞれのグループごとの重心（代表）におもりをぶら下げたてんびんの問題に置き換えてしまえばよいわけですね。

ぜひ、類題にチャレンジして見てください。

本日はここまで、ではまた〜（・◇・）/~~~