皆さん、こんにちは。
算数科のSです。

今回のテーマは「同じ文字がある順列」です。

 

早速、問題を見てみましょう。

問１．「さ」「く」「ら」「さ」「け」 の5文字を並べてできる順列は全部で何通りですか。

 

場合の数の基本は「書き出し」で手を動かすことですが、2つある「さ」の扱いに困りますね。
全部書き出して、同じ並びになったものを消すという手もありますが、見落としやすく危険です。

 

そこで、同じ文字がある順列について、2つの解法をご紹介しようと思います。
どちらが良いということではありません。
自分にとって理解しやすい解法を身につけていただけたら幸いです。

 

＜解法１＞ 最初に「さ」を置く場所を決めてしまう方法

 

まず、5文字を並べるための場所を用意し、2つの「さ」を最初に置いてしまいます。
5か所から2か所を選べばよいので、5×4÷（2×1）=10通りとなります。

次に、残った3か所に「く」「ら」「け」の3文字を並べればよいので、
全部で、10×（3×2×1）=60通り となります。

 

＜解法２＞ 「さ」に番号をふって区別する方法

 

2つの「さ」に番号をふり、「さ1」 「さ2」とします。
すると、「さ1」「く」「ら」「さ2」「け」の異なる5文字を並べる問題になりますので、
5×4×3×2×1=120通りの順列ができるのですが、
「さ1」「く」「ら」「さ2」「け」、「さ2」「く」「ら」「さ1」「け」 はともに「さくらさけ」という並びです。
2つ同じ順列ができてしまいますので、このままですと重複して数えていることになります。
「2つで1通り」と考えると、答えは120÷2=60通り となります。

 

次は少しレベルアップします。
問1の解法を踏まえたうえで、次の問2をご覧ください。

 

問2. 「さ」「く」「ら」「さ」「く」「さ」の6文字を並べ替えてできる順列は全部で何通りですか。

今度は「さ」が3つ、「く」が2つある問題です。問1と同じように問2も解いてみましょう。

 

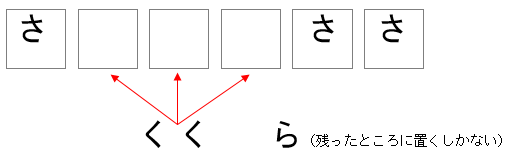
＜解法１＞ 最初に「さ」 「く」 を置く場所を決めてしまう方法

まず、「さ」を置く方法は、6か所から3か所選ぶので、6×5×4÷(3×2×1）=20通りです。
次に、「く」を置く方法は、残った3か所から2か所選ぶので、3×2÷(2×1)=3通りです。
最後に残った「ら」を置く場所は1通りしかないので、答えは 20×3=60通り となります。

 

 

＜解法２＞ 「さ」「く」に番号をふって区別する方法

「さ1」「く1」「ら」「さ2」「く2」「さ3」の6文字を並べてみると、6×5×4×3×2×1=720通りの順列ができます。ただし、「さ1」「さ2」「さ3」の入れ換えで3×2×1=6通り、「く1」「く2」の入れ換えで2×1=2通り同じ順列ができるので、6×2＝12個同じ並びが出てくることになります。

少しわかりにくいと思うので実際に重複したものを書き出してみます。

 

これら全部「さくらさくさ」の並びになっているものです。
このように、1つの並べ方に対して12個同じ順列ができるので12で割らなくてはいけないのです。

したがって、答えは 720÷12=60通り となります。

「同じ文字がある順列」いかがでしたでしょうか？
ちょっと難しかったかもしれませんね。

どちらかというと、このタイプは一行問題にあたるかもしれません。
サッと計算で処理できるといいですね。

それでは、また次回お会いしましょう！