こんにちは、算数を担当しております佐々木です。

本日は、前回の続きをお伝え致します。

前回までにお伝えしていたことは、
テストでの心がけです。

① 問題文をちゃんと読む。
② 何を使って解くかを見定めてから解き始める。
③ 問題文にでている条件を使っているか確認する。

短い文章の問題でも、長い文章の問題でも、
この3点に気を付けて問題文に当たってください。

それでは、本日は具体的に解いていきます。

(1)は、2つに分かれている文章の前半部分です。
以下の「ア」の部分から、

A店では、570個、B店で190個仕入れて利益が2店とも同じということから、
個数の比を求めて、1個当たりの利益に当たる金額の比が個数の逆比になるということをつかって
解きましょう。

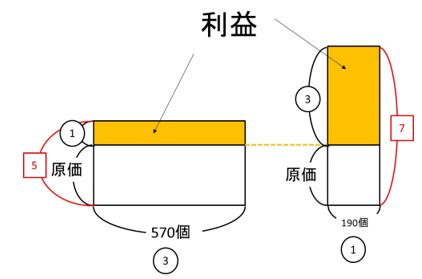
A店とB店の個数の比が570:190＝3:1
より、利益が等しいということから、利益の比は、①：③

また、定価の比がA：B＝1：1.4＝5⃣：7⃣
となり、

5⃣＝原価＋①
7⃣＝原価＋③

より、7⃣－5⃣＝③－①
2⃣＝②
ということにより、□の比と○の比が同じになるので、原価は⑤－①＝④とわかる。
A店の定価は⑤であるので、⑤÷④＝1.25倍

それでは、次に(2)は、

イの部分を使って解き進めます。

（2）まずA店だけに注目して解いてください。
問題文の「2日目は、A店では品物Xを□個仕入れて1日目の定価5％引きで売ったところ、すべて売ることができ、1日目と同じ金額の利益がでました。」

ここまでで、やはりまた、「同じ金額の利益」
とでているので、1個当たりの利益の比と個数の比が逆比であることを利用します。

A店は、⑤×0.95＝4.75の定価で売ったことになります。
4.75‐4＝0.75が2日目の利益の割合です。
1日目と同じ利益となってので、1日目の利益は①となるので、
①:0.75＝4:3
よって個数の比は、3:4
3が570個に当たるので、4＝760個

（3）今度は、

「B店では、A店よりも40個多くの品物Xを仕入れて1日目の定価の3割引きで売ったところ、やはりすべて売ることができ、1日目よりも3000円多くの利益を出すことができました。」

という文章のところを使って解きます。

（2）で求めたA店の個数を利用します。
A店は760個だったので、それよりも40個B店は多いということから、760＋40＝800個

そして、1日目の利益よりも3000円多いということに注目して、
1日目の定価が⑦なので、2日目は、⑦×0.7＝4.9
4.9‐4＝0.9・・・これが、2日目の利益の割合となるので、
190×③＋3000円＝800×0.9
720－570＝150・・・これが、3000円にあたるので、
①＝20円
原価は、20×④＝80円

皆さん、いかがでしょうか。

算数の問題も、文章を分析して、一語一句の意味を正確にとらえましょう。
そして、文章にでてきた数値、条件には○を付ける、線を引いて、
どの方針で解くかを見定めてから解くようにしましょう。

解き方は分かっているけれど、「気付けない」「何を使って解いたらいいのかわからない」という
お悩みをよく聞きます。

問題文の読み方、条件の使い方、ここを個別で見ていきます。

それでは、今回はこの辺で。
ありがとうございました。