みなさん、こんにちは。
受験ドクターの坂井智則です。
今回のお話はちょっと長くなりますので、いきなり本題に入ります。
問題の意味も分かるし、数えることができるので手も動くから答えも出る。
でも答えが合わない。
そんな問題の正解を30秒でやっつけてやろう!
なんていうお話です。
実はこれ、どこかで1度は見たことある問題ですよね。
正方形が全部でいくつできるか、正確な個数を答えることはなかなか難しいんです。
1個足りなかったぁ~。とか生徒が言っているのを私は何度も耳にしました。
みんな一生懸命に数えてくれるんですけど、どうしても拾いもれが出てしまうんです。
本気を出して数えても正確に数えられているのかいないのかもよくわからない・・・・
答えが合わない可能性を考えると他の問題に時間をかけたほうが良いのではないだろうか・・
でも解き方がわからない問題ではないので捨てるにはあまりにも惜しすぎる・・・・
そんな気持ちになってしまう問題の1つです。
今回のお話は、こんな悩みを抱えているみなさんの気持ちをすっきりさせてみようというお話です。 といってもなんてことはありません。間違えない数え方をみなさんといっしょに確認していくだけです。
ぜひお付き合いください。
結論: 1×16+2×9+3×4+4×1 = 50個
答えは50個です。
この式、どうやって考えているのでしょうか。
理屈がわかってしまえば、点の数が25個より多くても答えはすぐに出せます。
式も30秒で出来ます。
では考え方を見ていきましょう。
【考え方】
説明のなかに赤く塗った正方形が登場してきます。赤く塗った正方形は大きさにより分類すると 「①の種類」、「②の種類」、「③の種類」、「④の種類」の4種類です。
青の正方形も登場してきます。青の正方形は赤く塗った正方形の中に作ることができる正方形です。青の正方形ができるパターン数は赤く塗った正方形の大きさによって異なります。
これらを利用して作ることができるすべての正方形の数をかぞえていきます。
では具体的にどのように数えていくのかを見ていきましょう。
25個の点の中に赤く色を塗った正方形を作ります。
右の図は最も小さい大きさの赤く塗った正方形で
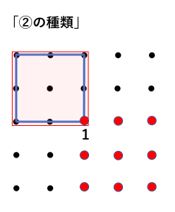
「①の種類」とよびます。
右の図で赤く塗った1×1の正方形の右下に赤い点を打ちます。
赤く塗った1×1の正方形を25個の点の中で移動させたとき、正方形の右下の赤い点に着目すると「①の種類」の赤く塗った正方形は16個(4×4)できることがわかります。
そして赤く塗った正方形の中にできる正方形は青の正方形1パターンだけです。
よって「①の種類」の赤く塗った正方形の中にできる青の正方形の数は16個です。
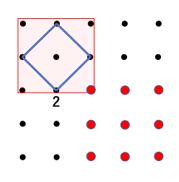
「①の種類」と同様に考えると「②の種類」の赤く塗った2×2の正方形は25個の点の中を移動させると9個(3×3)できることがわかります。
しかし、「②の種類」では、赤く塗った2×2の正方形の中にできる青の正方形は上の図と合わせて2パターンあります。
これらを合わせて次のように考えます。
赤く塗った2×2の正方形の正方形の中にできる青の正方形は2パターンですが、青の正方形の4つの頂点のうち赤く塗った2×2の正方形の下の辺と接する点に番号を付けて何パターンできるのかを数えることにします。
以上より「②の種類」の正方形の数は
2パターン×9個(3×3)=18個
よって「②の種類」の赤く塗った正方形の中にできる青の正方形の数は18個です。
「③の種類」は上の図のように赤く塗った3×3の正方形の中にできる青の正方形は3パターンあります。また、赤く塗った3×3の正方形は25個の点の中を移動させると4個(2×2)できることがわかります。
これらを合わせて考えると次のようになります。
青の正方形が何パターンできるのかは先程と同様に赤く塗った3×3の正方形の下の辺と接する点に番号を付けて数えることにします。
3パターン×4個(2×2)=12個
よって「③の種類」の赤く塗った正方形の中にできる青の正方形の数は12個です。
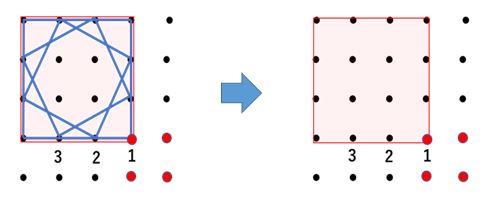
「④の種類」は上の図のように赤く塗った4×4の正方形の正方形の中にできる青の正方形は4パターンあります。また、赤く塗った4×4の正方形は25個の点の中を移動させると1個(1×1)できることがわかります。
これらを合わせて考えると次のようになります。
4パターン×1個(1×1)=4個
よって「④の種類」の赤く塗った正方形の中にできる青の正方形の数は4個です。
以上より、「①の種類」、「②の種類」、「③の種類」、「④の種類」を合計して
16+18+12+4=50 50個
1×16+2×9+3×4+4×1 = 50個
この冒頭で述べた計算の意味もご理解いただけたのではないでしょうか。
どうですか。50個を全て数えて求めてもよいのですがなかなか大変な作業です。
ところが今回のように4つの種類に場合分けしてから計算で求めると集計しやすくなることが分かったと思います。
では、最後に25個の点より点の数が多い問題を出して終わりにしますね。
ぜひ、挑戦してみてください。
それではみなさん、
またお会いしましょう。
【問題】
下の図のように100個の点が等しい間かくをあけて並んでいます。100個の点から4個の点を選んで、いろいろな大きさの正方形をつくります。正方形はいくつできるでしょうか。
9種類に分けて集計すると
答えは825個になります。