今回の「基本を考えよう」は「タレースの定理」です。「タレースの定理」
というと聞きなれませんが、

　　　　「直径に対する円周角は、直角である」

図で表すと

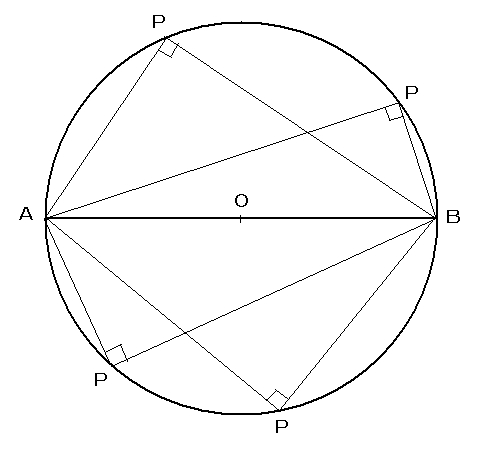
です。ＡＢが直径の場合、円周上のどの点Ｐをとっても、角ＡＰＢ(円周角)
は直角になります。みなさん、よくご存知ですよね。

これを「タレース(タレス、ターレス)の定理」と言います。

「タレースの定理」はこれだけでなく、「対頂角は等しい」「二等辺三角形
の底角は等しい」など５～６個の定理を指します。今では当たり前のことば
かりですが、紀元前６世紀ころのことです。

紀元前６世紀と言っても古すぎてピンときません(笑)。しかし、日本では当
時、弥生時代であることを考えると、タレースさんのすごさがなんとなく解
ります。

     タレースさんとはどんな人物か 

タレースさんは古代ギリシャの数学者、哲学者、科学者です。

地面に棒を立てて、その影の長さでピラミッドの高さを言い当て、王様を驚
かせただとか、日食を予言して有名になったとか、オリーブの豊作を予想し
て、一儲けしたとか、さまざまな逸話があります。

当時、エジプトでは測量術が高度に発達していました。しかし、それがどう
して正しいのか、誰も証明しておらず、興味もなかったようです。

タレースさんは、「なぜ、そうなるのか」を証明し、図形に論理を組み込み、
論理で世界を考えることを確立しました。

科学、哲学、数学の創始者として、ギリシャの七賢人の一人に挙げられてい
ます。

    なぜ、直径に対する円周角は、直角なのか

では、なぜ、直径に対する円周角は直角になるのでしょうか。

タレースさんは次のように証明しました。

まず、下図において、点Ｐと中心Ｏを結ぶ補助線を引きます。

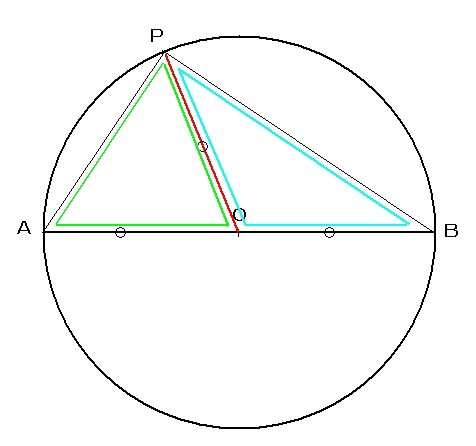
　　　半径はすべて等しいので

　　　　　　直線ＯＡ　＝　直線ＯＰ　＝　直線ＯＢ

　　　になります。

つまり、

　　　　　　三角形ＯＡＰ　と　三角形ＯＢＰ　は二等辺三角形

です。

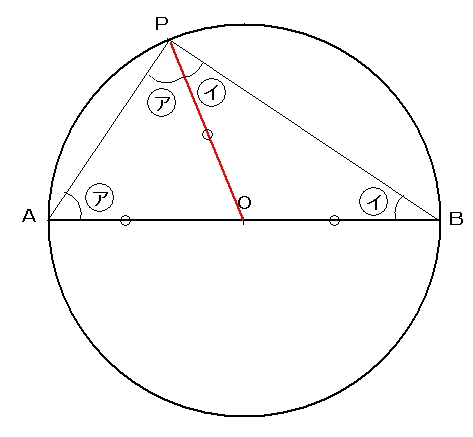
上の図のように二等辺三角形の底角は等しいですから

　　　　　　角ＯＡＰ　＝　角ＡＰＯ　＝　角ア

　　　　　　角ＯＢＰ　＝　角ＢＰＯ　＝　角イ

になります。

三角形の内角の和は１８０度ですから、

　　　　　角ア　＋　角ア　＋　角イ　＋　角イ　＝　１８０度

つまり

　　　　　（　角ア　＋　角イ　）　×　２　＝　１８０度

　　　　　角ア　＋　角イ　＝　９０度

になります。ですから

　　　　　角ＢＰＡ　＝　９０度

になるわけです。

今回の「基本を考えよう」は「タレースの定理」でした。