みなさん、こんにちは。　海田真凜です。

宣言通り、今回は算数について語ります。

早速ですが本題へ。

今回のお題は
「等差数列は3行で解く」　

では、いきましょう。

等差数列のお悩み

数列のなかで、中学入試で最もよく出題されるのが
等差数列。

5，8，11，14，17，・・・
こんなふうに、差が等しくなっている数列です。

お通いの塾により履修する時期は異なりますが
大抵は4年生のカリキュラムで登場します。

等差数列の授業を終えた4年生のご相談で多いのが
以下の内容。

等差数列の問題で「何番目ですか？」と問われると
答えが1だけズレていることが多い。
どうすれば修正できる？

等差数列の順番を求めたときに答えが1ズレるというのは
①植木算に基づく等差数列の構造が理解できていない
②いつもと逆の流れで物事を考えるのが苦手
のどちらかです。

原因が①であれば
植木算での「間の数」と「両端を含めた木の数」の関係を理解すること。
それが等差数列での「差の個数」と「並んでいる数の個数」の関係と一致します。

原因が②であれば
いつもと逆の流れで物事を追っていく練習を積み重ねていくこと。
今後、等差数列に限らず、別のテーマでも同様の問題が起こるはずです。
様々なテーマにおいて逆算が含まれる問題の演習を積んでいくことで
問題点が解消していきます。

ちょっとやり方を変えてみる

原因①②ともに対策をとりつつ
テストが目前で応急処置が必要なときには
以下の解き方を試してみてください。

合言葉は
等差数列は3行で解く！

問題

（１）
差が3の等差数列です。

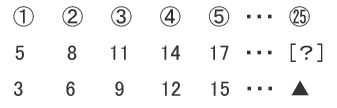
まずは、この数列を2行目にして
1行目に順番を丸数字で書いていきます。
こんな感じですね。

そして、3行目には「差×順番」の答えを書いていきます。

この場合、差が3なので
3（3×1），6（3×2），9（3×3），12（3×4），15（3×5），・・・となります。

では、25番目の数を考えてみましょう。

▲＝3×25＝75

ここで2行目と3行目を比べてみると
2行目は3行目より2大きくなっているので
[？] は75＋2＝77　となります。

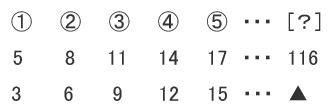
（２）
116は何番目？

3行目は2行目より2小さくなっているので
▲＝116－2＝114

3行目は「差×順番」なので
114＝3×[？]

よって、[？]＝114÷3＝38番目　となります。

等差数列は3行で解く！

この解法の特徴は
植木算の考え方を排除している点。

植木算の考え方が等差数列ではどうしても馴染まないのであれば
無理にこだわる必要はありません。

この3行処理を身に着けてください。

おしまい。

さて次回、何を書こうか思案中。

しばらく算数講師らしく算数を語ります。

それでは、また～