みなさんこんにちは。受験ドクターの桑田陽一です。
5月の講師ブログをお届けします。

令和元年が始まったと思ったのもつかの間、まもなく1か月が過ぎようとしています。
塾での新年度である2月、学校の新年度である4月に加え、今年は5月にも改元という気持ちを新たにする機会がありました。
元号の変わり目に際して、目標を立てた受験生もたくさんいるでしょう。そのときの気持ちは続いていますか？

私も、5月1日から小さな目標を2つ立てて、これまで何とか続けることが出来ています。小さな目標から、コツコツと頑張っていきましょうね。

さて今回は、前回お届けした「中学受験生でも解ける！？東大入試2019年版」の解説編をお送りします。

まずは、問題を確認しておきましょう。

2019年度　東京大学　文科　数学　第3問(改)

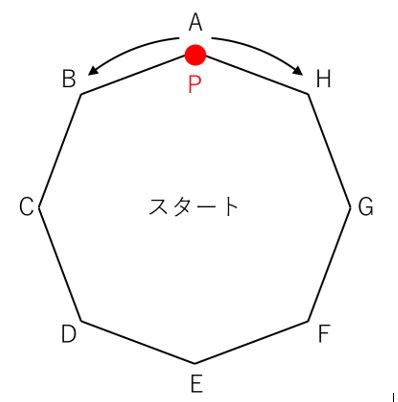
正八角形の頂点を反時計回りにA、B、C、D、E、F、G、Hとします。また、投げたときに表と裏が等しい確からしさで出るコインがあります。
点Pは最初に点Aにあります。
コインを投げ、表が出れば点Pを反時計回りにとなり合う頂点に移動させ、裏が出れば時計回りにとなり合う頂点に移動させます。
このとき、次の問いに答えなさい。

(1)コインを10回投げたとき、点Pが点Aにあるようなコインの表裏の出方は何通りありますか。
(2)コインを10回投げたとき、途中で点Pが少なくとも1回点Fに移動した上で、10回目には点Aにあるようなコインの表裏の出方は何通りありますか。

では、さっそく解説を。

(1)コインを10回投げたとき、点Pが点Aにあるようなコインの表裏の出方は何通りありますか。

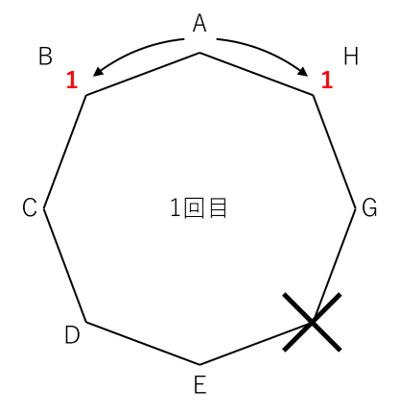
最初、点Pは点Aにあって、コインの表裏によって下図のいずれかの矢印のように動きます。

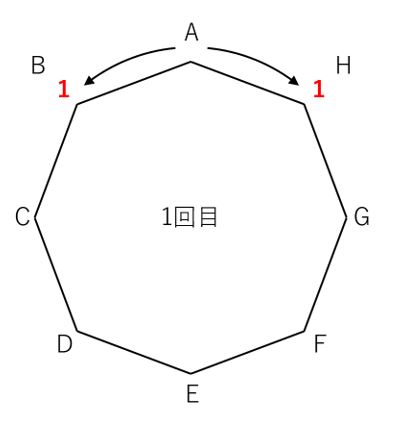
したがって、1回目のコインを振ったとき、Bにいるような出方とHにいるような出方がそれぞれ1通りずつ。
これを図に書き込んでみましょう。

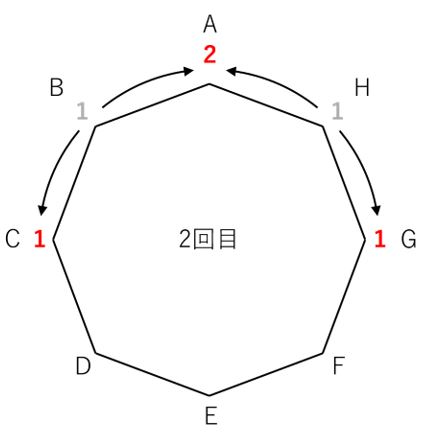
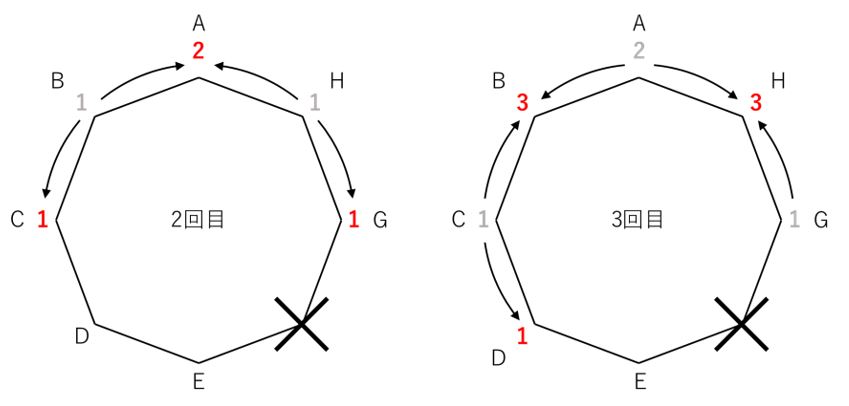
このあと、2回目のコインを振ると点BまたはHから下図の矢印のように移動します。

点Aに戻ってくるようなコインの出方は、点BまたはHからの2通り。
点Cに進むのは、点Bからの1通り。点Gに進むのは点Hからの1通りであることが分かります。
図には、2回振ったときの場合の数を赤で、前回の場合の数を灰色で示してあります。

3回目はどうなるでしょうか？

灰色で示した2回目の数値を経て、点B、D、F、Hのいずれかに移動します。
この中で、たとえば点Bに移動する場合には、2回目の時点で両隣のAかCにいたはずです。
したがって3回目にBに来る場合の数は、前回Aに書かれた2通りとCに書かれた1通りを加え、3通りです。
他の点についても同じように、両隣の点に前回書かれた場合の数を加えれば、今回の場合の数となります。
このあたり、「道順の問題」(受験ドクター　イメージde暗記　根本原理ポイント365　基礎編096)と似たところがありますね。

さて、要領がつかめれば、あとは単純作業です。一気に行きましょう！

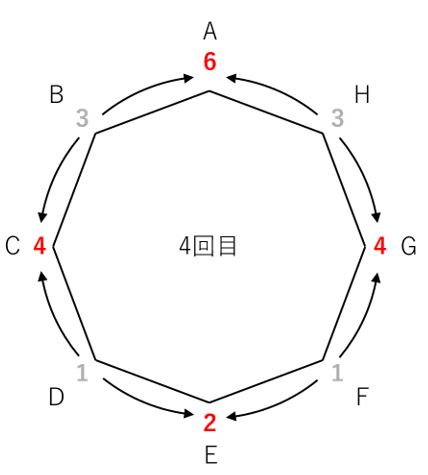
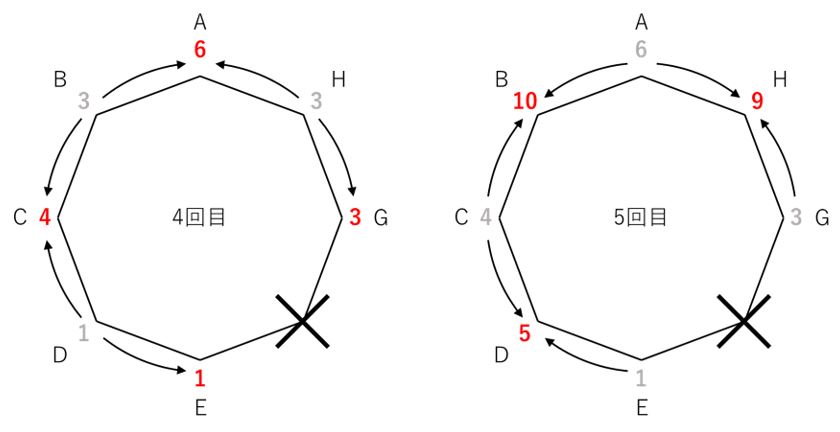
4回目。今回の赤い数値が、両隣の灰色の数値(前回3回目の値)の和になっていることを確認してください。

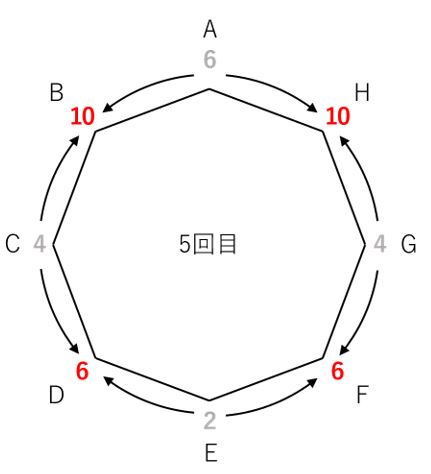
5回目。

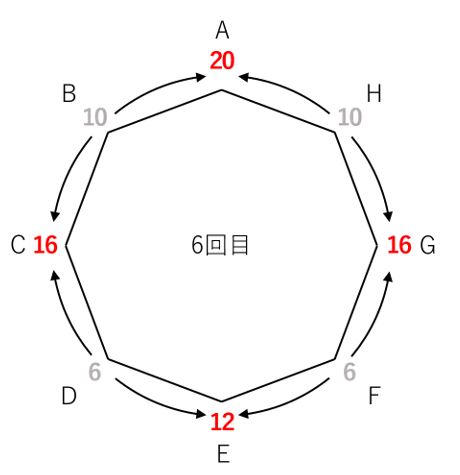
6回目。

7、8、9回目。

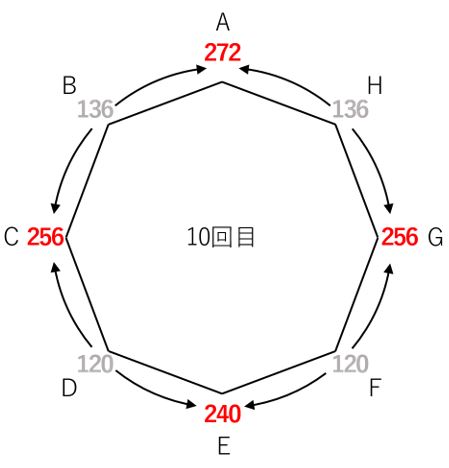
そして10回目！

と、これでようやく計算完了！図の点Aに書かれた272通りが答えです。

(2)コインを10回投げたとき、途中で点Pが少なくとも1回点Fに移動した上で、10回目には点Aにあるようなコインの表裏の出方は何通りありますか。

「(1)の解説を読んでみたら、(2)を考えられそうな気がする！」と思った人は、ここで読むのを止めてぜひ自力で挑戦してみてください。東大入試の問題を考えるなんて、ワクワクしませんか？

…
…
…
…

では、解説です！

「少なくとも1回点Fに移動」ということは、点Fに移動したのは2回かも3回かもしれません。
こんなときには、逆に「途中で点Fに移動しなかった場合」を考え、すべての場合の数から引いて求めるのが定石です。

(1)と同じような図ですが、点Fに移動しない場合を考えるので、点Fに×印をつけておきます。

2回目の図までは(1)と変わりませんが、3回目から×印の影響が現れます。
点Fは通れないので、3回目の図で点GからFに伸びる矢印はありません。

4回目と5回目。×印の影響で、(1)のときよりも小さめの数値が書き込まれることになります。

と、ここまで同じような図がたくさん並んでいるので、敢えて6～9回目の図を省略し…

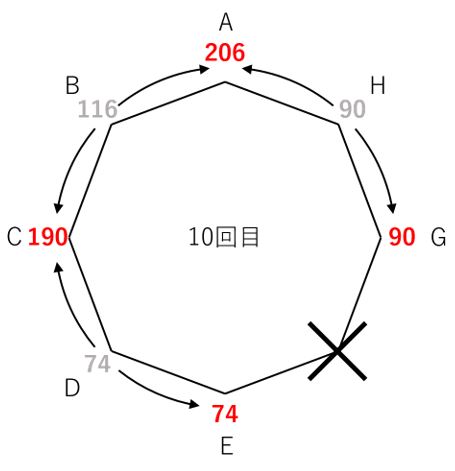
10回目まで作業を続けると、このような図が出来上がります。
意欲のあるみなさんは、自分でも確認してみてください。

よって、(2)の答えは図のAに書かれた206通り…ではありませんね。
いま求めたのは、「途中で点Fに移動しなかった」場合の数です。求めたかったのは、「少なくとも1回は点Fに移動した」上で10回目に点Aにあるような場合の数でした。
(1)の答えである272通りがすべての場合の数に当たるので、ここから引いた272-206＝66通りが(2)の答えということになります。

今年も東京大学の入試問題を楽しんでもらえましたか？
また何年後かに、同じテーマでブログを書けるときが来るかもしれません。そのときをお楽しみに。

今回はここまで。