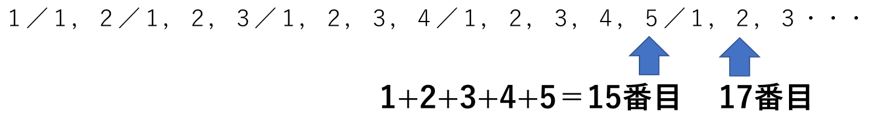こんにちは。受験ドクターのI.Sです。
今回は、規則性の中の、三角数を利用した「群数列」についてお話していきます。
次のような数列です。

１，１，２，１，２，３，１，２，３，４，１，２，３，４，５，・・・

この数列は、下のように区切ることが出来ます。

１／１，２／１，２，３／１，２，３，４／１，２，３，４，５・・・

斜線でグループに分けると、グループ内の数字の個数が１つずつ増えていくような数列です。
このような数列で

（１） 50番目の数は何ですか？
のような問題が出題されます。
さて、どのようにして考えていけば良いのでしょうか？また、ご家庭で指導される際に気を付けるべき点はどこなのでしょうか？　説明していきます。

まず、この種の数列は、各グループの一番右の数に特徴があります。例えば「5グループ目の最後の数は何番目ですか？」のような問があったとします。
この場合、下の図のように、1+2+3+4+5＝15　と、計算で求めることが出来ます。

では逆に「15番目の数は何ですか？」という問題があったとします。
すると、1+2+3+4+5＝15　なので、15番目の数が5グループの最後であることが分かります。15番目の数は5です。

では、17番目の数でしたらどうでしょうか。15番目が5グループの最後なので、17番目はその次、6グループの2個目の数だと分かります。つまり、答えは2です。

つまり、この種の数列では、各グループの最後の数が何番目かは計算で求められるので、グループの最後の数が重要です。グループの最後の数のことを、私は目印と呼んでいます。
求めたい数から近くにある目印を探すことが、この問題で取るべき最初の行動なのです。

最初の問に戻ります。
（1）50番目の数は何ですか？

考えていきましょう。
まずは、50に近い目印を探していきます。すると
1+2+3+4+5+6+7+8+9＝45　というものが見つかります。
つまり、9グループの最後の数は45番目だということが分かります。
求めるのは50番目ですので、この目印の5つ後だということになります。
9グループの最後の数の、5つ後ですので、50番目は、10グループの５　番目の数と言うことになります。
よって答えは「5」です。

もう1問行きましょう
(2)2回目に8が出るのは何番目ですか？

この問題も「目印」を元にして考えていきます。1回目に8が出るのは、8グループの最後です。2回目の8は、9グループの最後から2番目の所です。これが何番目かが問われています。
では同様に、近くの目印を探しましょう。9グループの最後から2番目から最も近い目印と言うと、当然9グループ目の最後の所でしょう。これが何番目かは、計算で求めることが出来ます。
1+2+3+4+5+6+7+8+9＝45　より、45番目です。求めるものは、これの1個手前なので、答えは44番目となります。

いかがでしょうか。この「目印」という言葉でグループに意識付けをすることで、何を考えれば良いのかが分かりやすくなります。つまり、近くにある目印を探し、そこから～個前、～個後、のように考えていけば良いのです。

大人が解く際には、上で説明したような手順を自然と頭の中で構成し、論理的に計算できるかもしれません。
しかし、小学生には、ここまで長い論理を脳内で構築することは大変です。
そのため「目印」のようなネーミングで具体化し、中間目標を作ってあげることが必要です。
いきなり50番目の数を求めようとするのではなく、まずは目印を探すと意識をスライドさせることで、結果的に答えに近づくことが出来ます。
解法の中に潜む、適切なポイントを中間目標として言語化してあげることも、中学受験生には必要な指導となります。
是非ご家庭でもお試しください。