みなさま、こんにちは。
受験ドクター算数科のHH講師です。

本日は、わり算のあまりと等差数列の問題の解き方についてお伝えしたいと思います。

算数の得点力は、根本原理・イメージ、力の使い分けと計算力だと考えていますが、このブログでは、根本原理・イメージと力について具体例をお見せします。

例題1）
4でわると1あまり、5でわると3あまる2けたの数で最も小さい数と、最も大きい数をそれぞれ求めなさい。

「根本原理」
4でわると1あまる、5でわると3あまる数字は、わる数である4と5の最小公倍数ずつ増えていく。

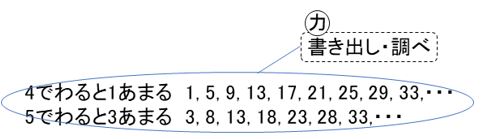
まず、書き出しの「力」を使って、調べます。

それぞれあまりから書き出し、4ずつと5ずつ増やしていきます。
この作業をおろそかにし、結果間違えるということがあります。
面倒くさがらず書きましょう。

力として、書き出し・調べの力を使っています。
書き方がわからない場合は、下の例を参考にしてください。

次に、同じ数字に着目します。
同じ数字には規則があります。
下の図の見てください。

13や33が4でわっても1あまり、5でわっても3あまる数です。
13と33の差は33－13＝20ですが、これはわる数4と5の最小公倍数になっています。
この規則を使って、13と33の次に条件にあてはまる数を下の図のように調べます。

以上のことから、求める答えはもっとも小さい数が13、もっとも大きい数が93です。

「イメージ」

このように、算数の問題は、根本原理に基づいて作られており、処理などを映像化したイメージと力（数十種類あり）を使って解くことが出来ます。

算数の学習は、まず第一に根本原理・イメージを紐付けながら覚えること、第二に問題によって力を使い分けられるように訓練することが必要です。
もちろん計算力も必要ですが、計算の工夫などイメージで覚え、訓練していくという点は同じです。

では、条件が増えた問題も解いてみましょう。

例題2）
4でわると2あまり、7でわると3あまり、9でわると4あまる1000に一番近い数を求めなさい。

まずは、先ほどお伝えしたイメージで書き出しを行いますが、3つの数字がそろうところをそう簡単に見つけることが出来ません。
もちろんこのまま書けば、同じになる数字が出てきますが、作業量が多くなってしまいます。
こういった場合は、まず2つに絞って調べると素早く問題を解くことが出来ます。

4でわると2あまり、7でわると3あまるもっとも小さい数は10だと見つけられます。
10の次は4と7の最小公倍数の28ずつ増えていきますので、
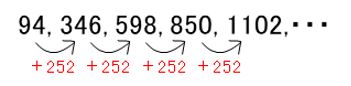
10, 38, 66, 94,・・・となります。
この内、9でわると4あまる数を調べると94÷9＝10・・・4より、94であることがわかります。
つまり、4でわると2あまり、7でわると3あまり、9でわると4あまるもっとも小さい数が94となり、これ以降4と7と9の最小公倍数の252ずつ増えていきます。
では、1000に一番近い数を調べましょう。

1000の前後は850と1102ですが、1102の方が1000との差が小さいため、1102が1000に一番近い数です。

「イメージ」

いかがでしたでしょうか？
わり算のあまりと等差数列の問題の解き方について、根本原理・イメージと力に分けて書きました。
簡単に言ってしまうと、根本原理・イメージが問題の解き方の大枠で、力が求められるひらめきです。

力は和や差、一定に着目する力など数多くあり、今回は全てをご紹介することはできませんが、一見目には見えないものです。
この力を明文化し、意識して使うことで、今まで漠然とひらめきと呼ばれていたものを鍛えることが出来、様々な問題を考え抜くことができるようになります。

では次回、またお会いしましょう。