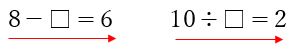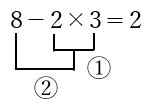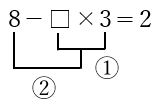みなさま、こんにちは。
受験ドクター算数科のHH講師です。

本日は、逆算についてお伝えしたいと思います。
算数の計算問題で失点してしまう場合、逆算の解き方を完全にマスターできていない場合があります。

「あとこの1問さえ解けていれば・・・」

その1問が逆算を含む計算問題だったことありませんか？

このブログでは、逆算のパターンについて例題を用いて確認していきます。
侮ることなかれ、逆算を解くときの思考プロセスはとても重要です。

基本的に逆算は、8つのパターンに分けることが出来ます。

【全8つのパターン】
①□＋3＝5
②□－6＝2
③□×2＝6
④□÷5＝4
⑤3＋□＝7
⑥7－□＝2
⑦5×□＝10
⑧6÷□＝2

「これくらいならわかるよ」「簡単すぎる」と声が聞こえてきそうですが、この形が最も重要で、分からなくなったときに立ち戻るべき基本問題です。

①～④は□が前にきている逆算の式で、逆の計算を考える事で求める事ができます。
①～④の解答は、次のように求めます。

①＋3の逆 →　－3を行い、□＝5－3＝2
②－6の逆 →　＋6を行い、□＝2＋6＝8
③×2の逆 →　÷2を行い、□＝6÷2＝3
④÷5の逆 →　×5を行い、□＝4×5＝20

⑤～⑧は、□が後ろにきている逆算の式です。
⑤～⑧の解答は、次のように求めます。

⑤3＋の逆 →　－3を行い、□＝7－3＝4
⑥□の前の数字から2をひいて、□＝7－2＝5
⑦5×の逆 →　÷5を行い、□＝10÷5＝2
⑧□の前の数字を2で割って、□＝6÷2＝3

御覧の通り、⑥と⑧のみ、前からそのままひき算と前からそのままわり算になっています。
下のようなイメージですね。

私が担当しているお子様には、「－□と÷□は要注意、前からそのままひき算わり算だよ」と教えています。
理論上、この8パターンの型をマスターすれば、どんな問題も解けます。
8つのパターンが確認できましたので、次に間違えやすいポイントをご紹介します。

【間違えやすいポイント】
①計算順序を間違えてしまう。
②□を求めるときの計算式を誤ってしまう。

【①の具体例】
基本となる計算問題を解いてみましょう。

例題　8－2×3＝

計算の答えは、2ですね。
この答えを18と求めてしまった場合は要注意です。
計算の順序を考えるときの頭の中のイメージは、以下のようなものです。

答えを求めるためには、①→②の順に計算をしますが、計算の順序の基本が抜けていると逆算の計算順序も誤ります。

8－□×3＝2は、本来であれば①8－2＝6②6÷3＝2と□＝2を求めます。
先述した計算の順序の基本が抜けていると、①2÷3＝②8－と誤った答えを求めてしまうこともあります。

計算の順序がわかっている場合、逆から考えることを意識して問題を解いてみましょう。

「①の部分が先に計算され、次に②の部分が先に計算される」というところまで、突き止められるようになったら、8－□＝2を考えてみましょう。
ここまで考えられると、8つのパターンに落とし込むことが出来るので、□に当てはまる数は8－2＝6と求めることができ、□×3＝6になることがわかります。
すると、□に入る数は6÷3＝2と求めることできます。
簡単な例で説明を行っていますが、これは分数や小数が含まれている場合も同様です。
お子様の答案を確認し、状況によっては計算の順序の理解度から確認する必要があります。

【②の具体例】
例題　
正答　
誤答例　

このような間違いは結構多いです。
本来4をでわらなければならないところですが、誤答例はを4で割ってしまっています。
逆算の8つのパターンを使いこなすことが出来ていると、このような間違いは起こりませんが、あまり深く考えずに逆算の問題を解いているだけの状態だとこのような失敗が出てきます。

【逆算まとめ】
長々と書きましたが、上記をまとめます。
やることは3つです。

①8つのパターンでルールを知る。
②計算の順序の理解度が完璧か確認する。
③①で知ったルール通りに計算できているかチェックする。

計算ミスなどで失点している場合もありますが、理解度が低く得点できていない場合は①～③のどこかで引っかかっている状態です。

①は具体例を見せる事ですぐに理解できますが、その運用がうまくできないと③で引っかかってしまいます。
慣れるまでは8つのパターンのどれに当てはまるかを考えるようにし、訓練を積んで解答スピードを上げられるようにしましょう。

ではまた次回お会いしましょう♪