みなさん、こんにちは。受験ドクター算数科のA.K講師です。

さて、前回こんな問題を出しましたね。

【問題】
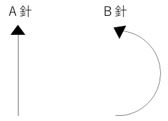
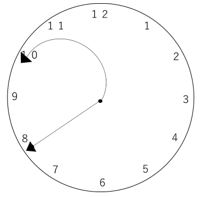
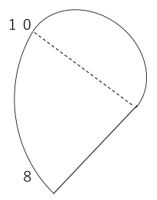
下のようなA針とB針があります。

Ａ針は直線の形をしており、長さは１２㎝です。Ｂ針は半円の形をしており、直径は１２㎝です。
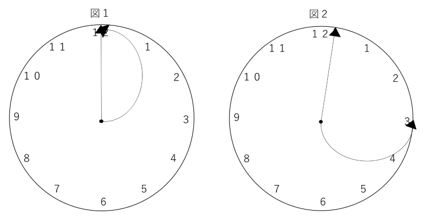
この２つの針を、半径が１２㎝の円の中心に取り付け、時計を作ります。Ａ針は時計の短針と同じ動きを、Ｂ針は時計の長針と同じ動きをします。下の図１は１２時の状態を、図２は１２時１５分の状態を表しています。

このとき、２つの針と時計の円周とで囲まれた部分の面積について考えていくことにします。（ただし、両針の先端についている矢印の部分は、面積を求める時には考えないものとします。）また、円周率は３．１４とします。
（１）５時のとき、２つの針に囲まれた部分において、文字盤の３の数字が含まれる部分の面積を求めなさい。
（２）７時５０分のとき、２つの針に囲まれた部分において、文字盤の９の数字が含まれる部分の面積を求めなさい。
（３）８時から９時の間で、２つの針に囲まれた部分が半径６㎝の半円と合同になる時刻を求めなさい。

今回は、その答え合わせをしましょう。
（１）まずは問題文の指示に従い、実際に時計の図を描いてみましょう。

上図のようになり、文字盤の３を含むので右側の面積を求めることになります。時計の中心から文字盤の１２に向かって直線を引いてみると、

半径１２㎝のおうぎ形から、半径６㎝の半円を引けば良いことが分かりますね！
よって、１２×１２××３．１４－６×６××３．１４＝（６０－１８）×３．１４＝１３１．８８㎠となります。

（２）引き続き、問題文の指示に従うと以下のようになります。

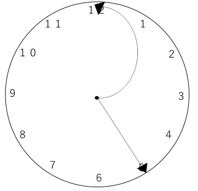
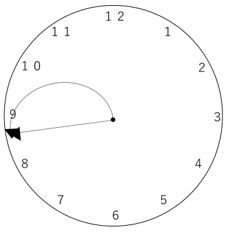
７時「５０分」ですので、短針の位置が文字盤の８の少し前にくることに注意しましょう！時計の中心から文字盤の１０に向かって直線を引いてみると、

半径６㎝の半円と、半径１２㎝のおうぎ形を足せば良いことが分かりますね！おうぎ形ですが、Ａ針（＝短針）が１分で０．５°ずつ進むことを考えると、７：５０から８時までは１０分間なので０．５×１０＝５°、８時から１０時までは３０×２＝６０°あります。合計すると５＋６０＝６５°となり、円全体のであることが分かります。
よって、６×６××３．１４＋１２×１２××３．１４＝（１８＋２６）×３．１４＝１３８．１６㎠となります。

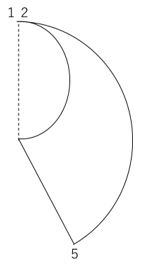
（３）合同になるということは、２つの針に囲まれた部分の形が直径１２㎝の半円＝Ｂ針と同じ形になるということです！最も簡単な例は、下のような１２時ぴったりの状態です。

これは、A針の先端とB針の先端が重なった状態なので、B針を通常の時計と同じ長針と見立てると、長針と短針が重なった時刻であると言えます。
一見、複雑な情況であっても、
「よく見てみると何ということがなかった、通常の問題の考え方と一緒だった。」
ということは算数では往々にしてあることなんですね。
したがって、求めるのは８時から９時の間で下の状態…

問題文を言い換えると
「（通常の時計算で）８時何分に時計の長針と短針が重なりますか？」
という典型的な問題に早変わりです！
よって、３０×８÷（６－０．５）＝２４０×＝となり、８時分が答えとなります。
～本日のまとめ～
・これまでに目にしたことがないような設定の問題だとしても、そこに書いてある例をよく読んだり、場合によっては自分で簡単な例を書き出してみてルールを把握するようにする。
・合同とは、図形同士の形・大きさが同じであるということ。
・難しい設定の問題であったとしても、中身は普段から学習していることと同じ内容であることが多いので、根気強く考える癖をつけるようにする。

今回はここまで。
次回は、ふたたび今年の入試問題について触れていく予定です。

ではまた、お会いしましょう♪