RS先生
できないなんて、
やってみないとわからない!
中学入試は4教科全てが大事なのはいうまでもありません。ですが、「中学受験といえば算数」というイメージをお持ちの方も多いのではないでしょうか。算数がことさら注目を引く理由は、算数という科目の特殊性と難しさにあると思います。算数は他の科目と違い、同じテーマを何度もくり返しながらだんだんとレベルアップさせていく科目です。また、あるテーマの理解が、別のテーマの理解の土台になっていたり、複数のテーマが融合し合って別のテーマを形成していたりと、非常に複雑な構造をしています。
このような特性をもった算数という科目ですから、身につけるには4年生~6年生という非常に長い時間が必要になるわけですが、もう一つ重要な事があります。
それは、教える側のスキルです。
子供は、その時々において本人が使える考え方、概念を総動員して、1つのテーマを理解しようと頑張ります。ですが教える側の大人は、長く生きてきた中でその問題を解決する別の考え方や概念を身につけてしまっていることがあります。本来土台として習熟しておくべきテーマ、他のテーマとの関連性など、本来は一歩ずつ理解の階段を上がっていかなければならないところに、一足飛びにその場しのぎの教え方をしてしまうことは、子どもの算数力の土台を不確かなものにしてしまいかねません。確実に算数力を積み上げていくには、算数という科目の特性を正しく理解し、子どもの発達の段階に合わせた適切な指導を行える大人が必要なのです。
分かりやすい例として、有名な「つるかめ算」という文章題を取り上げてみましょう。
実はつるかめ算は、数式としては中学2年生で学習する連立方程式に帰着していきます。従って4年生、5年生段階で習うほとんどのつるかめ算は、つる=x匹、カメ=y匹とおいて、頭の個数と足の本数に関する2つの式を立てるというような方法で解けてしまいます。
ということは、子どもにつるかめ算を解かせるには、連立方程式を立てて解くスキルだけを身につけさせればいいということになってしまいます。
もちろんそれでは、まったく中学受験には太刀打ちできないことはご存じの通りです。
つるかめ算は、解き方も多彩で、それぞれの解き方に他のテーマに繋がる重要な基本事項を含んだ奥の深いテーマです。一般的なつるかめ算の解法は、①交換法、②面積図があり、その他に③消去法(連立方程式)、④平均法といった方法もあります。
①交換法とは、「極端な状態をあえて作り、1個ずつ交換していくことで正しい状態に近づけていく」という考え方です。この考え方は、表を書いて数字の変化を1つずつ調べていく「規則性」の考え方につなげることが出来ますし、図形の問題でも活躍することがあります。
また、②面積図は、「たて×横=面積」というかけ算を「1匹あたりの足数×頭の数=足の合計数」というかけ算に置き換える考え方です。
面積図はつるかめ算だけでなく、速さや平均といった「A×B=C」の形をしたほとんどの文章題に適用して考える事ができます。
もちろん、全てのことをいっぺんに教えることは不可能ですので、同じつるかめ算というテーマに何回も触れる事で、少しずついろいろな考え方を身につけていくことになります。
実際の入試問題では、一目で「〇〇算」と分かる問題が出ることはまずありません。しかし、出題されるほぼ全ての問題は、子供たちが学習してきた様々なテーマを組み合わせて解けるように作られています。もちろん中には鋭いひらめきが求められる問題が出題されることもありますが、そのような問題が合格・不合格を左右する問題になることはまずありません。算数を適切に指導するというのは、算数という科目の全容を把握し、各テーマの横のつながりまでを意識した教え方ができるかということになります。
█ 算数で伸び悩む原因
つるかめ算というひとつの文章題をとってみても、上記のような様々な要素を含んでいます。集団塾ではこれらを効率よく学習出来るようなカリキュラムが組まれてはいますが、実際に教えている先生がまだ新人であれば、算数という科目の全容を把握できておらず、必要なことをきちんと教えていないケースも考えられます。また、授業中に触れていたとしても、それを聞いているお子さんが、そのポイントを聞き逃しているかも知れません。聞き逃していることが毎回の授業で1回でもあれば、月に10個になります。1年で100個以上です。これだけのポイントが抜ければ成績への影響は甚大でしょう。ですが、集団授業というのは、その性質上クラス全体に必要なことを教えて、必要な学習をきちんと消化しきっている子をテストでふるいにかけながら引き上げていく・・・というスタイルをとるしかありません。
「5年生になってから算数の成績が落ちてきた・・・」、「塾で指示された内容は、ちゃんと家でも勉強しているのに、成績が伸びない・・・」、といった問題は、テーマ間の横のつながりが多くなる、5年生の前半から起こりやすくなってきます。4年生までは単元毎に授業を受け、出された課題をしっかりこなしていればそれなりに成績は維持・上昇します。しかし、5年生からは同じ方法でやっていても、教え方と本人の学習の仕方がまちがっていると、どんどん問題が顕在化してくることになります。ところが、今まで上手く行っていたことで、問題の所在に気付きにくくなってしまうのです。
「これまで上手く行っていたんだから、同じ方法で上手く行くはずだ」、「足りないのは本人の努力だろう」といたずらに学習量を増やしても問題が解決することはありません。塾から指示される課題は、多くの子どもにとってはそもそもキャパシティオーバーであり、スランプに陥っている子どもにそのようなやり方で解決しようとしても、状況の悪化に拍車をかけてしまうだけです。分かったような、分からないような中途半端な状態で、どれだけたくさんの基礎問題をこなそうが、見よう見まねで難問に取り組もうが、その子の力が上がることはありません。本人が自分でテーマのつながりを発見し、基本事項を整理しながら学習を進めるか、または適切な指導者が適切な指導を行いながら引き上げていく、そのどちらかしかありません。
█ どうすれば成績が上がるのか
以上の事を踏まえた上で、算数の成績を上げていくのに必要なことは次の3つのステップです。
① つまずきの原因を探る
つまずきの原因はお子様によって、上に述べてきたような指導スキルに起因するもの、本人の学習のリズム、あるいは本人の未熟な処理能力に起因するものなど様々にあり、またそれらが複雑に絡み合っていることもあります。このような問題に対し、的確に原因を見つけ出し、解決策を示していく必要があります。
② 正しい取り組みの道を提示する
塾から与えられた問題に全て取り組むというやり方は、お子様にとっては最適な方法ではありません。もし、根本的に理解が不足しているのなら、いくら問題を解いても、一人で出来るようにはならないでしょう。まちがったフォームでいくら素振りを練習してもバッティングが上達しないのと同じことです。まずは、課題をお子様にとって最適な量に絞り込み、まずはその問題をきちんと根本から理解することに努めます。さらに、復習を計画し、学習したことが効率的に定着していくように中、長期的な学習計画を作成します。「こういうふうに頑張ればかならず出来るようになるんだ!」というように、具体的道筋を見せてあげれば、お子様も前向きな気持ちになって取り組む事ができるようになるはずです。
③ 本人と一緒に目標に向けて伴走する
小学生はまだまだ孤軍奮闘して一人で頑張れる年齢ではありません。道筋が見えたとしても、その目標に向けて一緒に頑張ってくれる伴走者がいなければどこかで糸が切れてしまいます。中には一人でも目標に向けてたくましく頑張っていく小学生がいるかも知れませんが、私が何百人と指導してきた中でそのようなお子さんに出会ったのは、片手で数える程度しか思い出せません。大多数の中学受験生は、適切な大人のサポートがあって、はじめて中学受験という困難を乗り越え志望校合格をつかみ取ることができるのです。
█ 算数は楽しい!
中学受験は大変な道のりです。それを大変なものにしているのは、大部分が算数のため・・・とも言えるのですが、算数は大変がゆえに、実はとても面白い科目でもあります。
基礎的な力を備え、いろいろな難問へチャレンジできるようになってくると、算数という科目はワクワクとドキドキに満ちた、とても魅力的な世界でもあるのです。
ここでは、実際の入試問題を取り上げて、私の指導法の実例ということで、難問を解く醍醐味を一緒に味わってもらいましょう。
【麻布中学校 算数入試問題より】
問題
1辺の長さが1㎝の黒と白の正方形を図のように敷き詰めます。このとき、(1)~(3)の各図形の太線で囲まれた部分について、黒(斜線)の部分と白の部分の面積はどちらがどれだけ大きいか、それぞれ求めなさい。
(1)三角形ABC
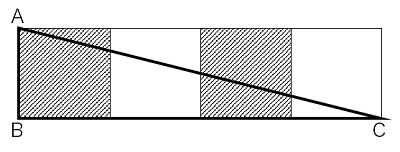
解法
これは麻布を受験する生徒であれば、難しい問題ではないでしょう。
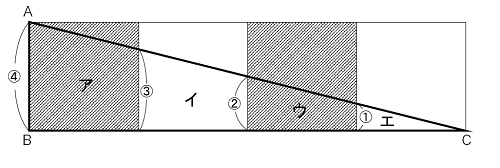
小さい三角形から順に1:2:3:4の相似形になっているので、AB=④として、上のように数字を書いていきます。
このとき、正方形1つを「台形」と見立てると、④+④=⑧=1㎠と表すことができます。

黒い部分
ア=③+④=⑦
ウ=②+①=③
合計⑩
白い部分
イ=③+②=⑤
エ=①
合計⑥
従って、黒い部分のほうが⑩―⑥=④ 多いと分かります。
⑧=1㎠ でしたので、④=0.5㎠ です。
答え:黒い部分が0.5㎠大きい
(2)三角形DEF
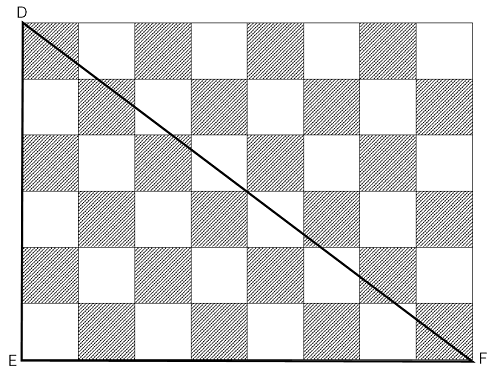
解法
ここから少し難しくなります。
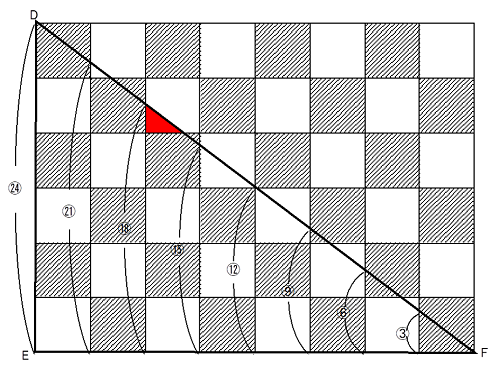
(1)で正方形1辺を④と決めましたので、DE=㉔などとおいて、先ほどと同じような方法で解くべきでしょうか・・・?
ここで一つ問題が発生しています。例えば上の図で赤く塗った三角形は、横の長さが正方形の1辺でなくなってしまっています。(他にもあります)
従って(1)と同じ方法で解こうとすると、横の長さも比で表さなければならなくなってしまって、計算量が非常に多くなってしまいます。
この問題に限れば、そのような計算方法も解法としては有効なのですが、余分に時間がかかってしまうことは否めません。また、時間も押し始めている後半の問題でもあります。
うまい方法はないでしょうか・・・?
いきなり計算をはじめてしまう前に、少し落ち着いて図形を観察してみましょう。
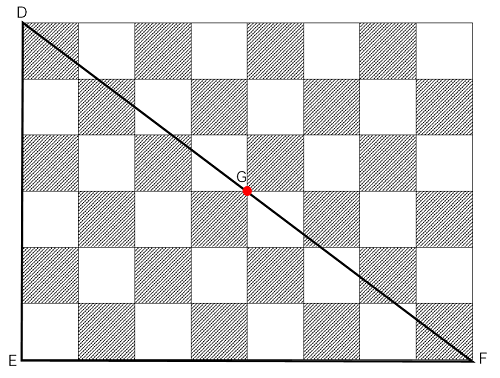
この図形は、横8個、縦6個の正方形で出来ているので、真ん中のGを中心として、対角線DFが点対称の位置関係にあることに気付きます。
点対称ということは、左側にあるものは右側に、上にあるものは下に動かす「等積移動」が使えるということです。
その視点でこの問題を眺めてみると・・・
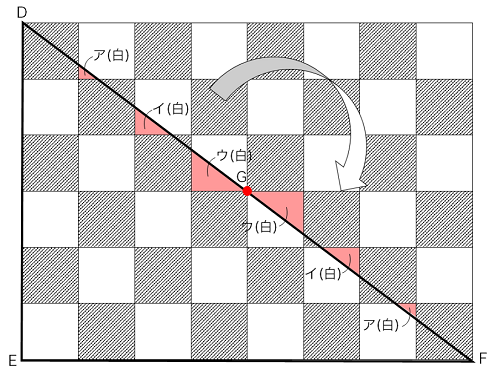
白ア、白イ、白ウと印をつけましたが、対称の中心Gで180°回転させ、反対側に持ってくることによって、中途半端なかたちだった白は、すべて正方形1枚に直せることがわかります。
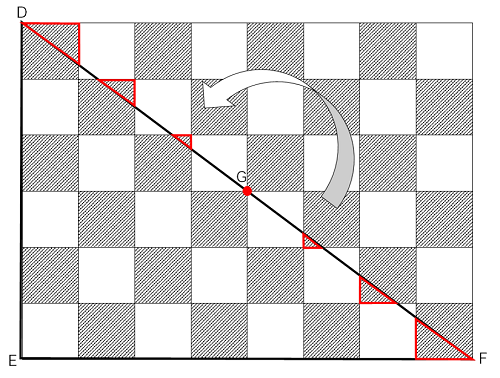
黒についても同様の移動が可能です。
以上から、正方形の大きさを①とすると、
黒の部分(左から)=③+③+②+②+①+①=⑫
白の部分(左から)=③+②+②+①+②+①+①=⑫
従って、黒と白の面積は同じであることが分かりました。
答え:黒い部分と白い部分の面積は等しい
(3)四角形GHIJ
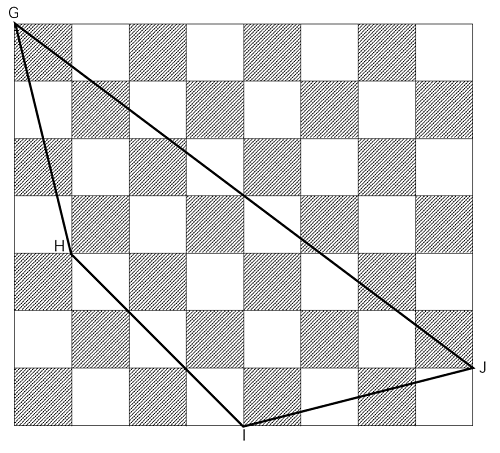
解法
さて、最後の問題です。
見るからにややこしそうですね・・・これも時間があれば計算のゴリ押しで何とかなりそうな気はしますが、試験時間内に手を出すと大やけどを負ってしまいそうな感じの問題です。
ですが、また図をよく観察してみましょう。実は(2)の結果をそのまま利用できる部分があるのです。
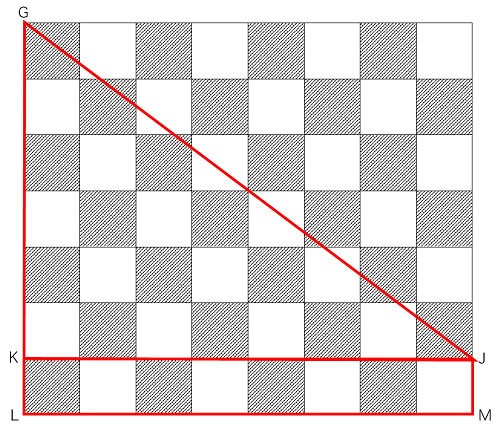
まず、全体をこのように捉えてみましょう。
△GKJは、(2)で解いたものと同じことにお気づきでしょうか。
(2)の結果から、△GKJにおいては黒と白の差は0㎠ということが分かっています。
その下の長方形KLMJについても、黒と白が同数あるので、図形全体において黒と白の差はありません。
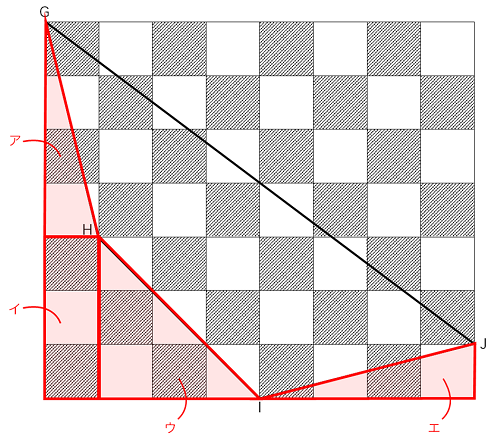
従って四角形GHIJの黒白の差は、上の図の赤く囲ったア、イ、ウ、エの図形で黒と白のどっちを多く引くかによって決まります。
アとエは(1)で解いた図形の白黒逆になっているので、白が0.5㎠×2=1㎠多くなります。
イは黒が1㎠多い、ウは白が0.5㎠多いとすぐに分かります。
以上より、ア、イ、ウ、エを通して、白の方を0.5㎠多く引くことになるので、
四角形GHIJは黒が0.5㎠多いということが分かります。
答え:黒が0.5㎠大きい
いかがでしょうか。
(2)で力技で解くという方向性ももちろんあるのですが、他の問題との時間配分を考えると、やはり上記の解法がベストと言えます。
また、(2)で力技へ舵を切った生徒は間違いなく(3)も同じ方向へ舵を切るはずですから、二重に時間を食うことになってしまうでしょう。あるいは諦めざるを得ないかも知れません。もしかしたら合否に大きく影響することになったかも知れませんね。
考え方は、非常に単純なものですが、これを実際の試験の場で解けるようになるには、基本的な問題を通して相当の練習を積むこと、また出題者が用意している解法への手がかりを察知する勘所も養っていく必要があります。
とても大変な道ではありますが、だからこそやり甲斐も有り、このような一見複雑に見える問題を、スパッとシンプルに解いたときの快感は他の科目ではなかなか味わうことが出来ません。
受験生の皆さんには是非この快感を一緒に味わっていただきたいと思います。
私たち受験ドクターのプロ講師陣が全力でサポートさせていただきます!

