計算力

算数の力を築き上げるために必要なのは、まず計算力です。計算力がないと新しい単元内容を学習するたびに実力養成に弊害をもたらせます。効率よく学習するためには、新しい学習内容の本質部分の理解に力を注げるかが重要です。計算力がないと問題を解く都度、途中の計算で手が止まり、自然と計算を解くことに多くの力が注がれていってしまうのです。

5年生にもなると、学習量も増えてスケジュールもタイトになってきます。その限られた時間の中で宿題や復習を行っていかなければなりません。例えば塾で学習した内容を1～２時間かけて復習が完結できる生徒がいる一方、やる気はあっても計算力がないために正解までなかなかたどりつけなかったり、そのために集中力が途切れてしまったりするため、本質部分の学習が思うように進まず、１週間の学習内容が未消化になってしまうこともあるでしょう。もし、後者の悪循環が半年も続けば生徒自身も算数が得意科目だと思えることは難しくなるでしょう。

では、どのレベルであれば計算力があるといえるのでしょうか。

（３年生）①2桁＋1桁　，２桁－１桁の計算の答えが瞬時（暗算です）に答えられるか。
　　　　　②掛け算の九九がどこを聞いても即答で答えられるか。

＊①の２桁とは11～20までで大丈夫です。ただし、繰り上がりや繰り下がりがある足し算と引き算を前提とします。
　例えば、15＋8＝　17－9＝　といった計算です。

②８×7は？　と聞いたとき、もし8×1＝8　8×2＝16　8×3＝24　・・・・と順番に考えることをしていたら、生徒は割り算でかなり苦労するケースが多いです。

この２点がクリアできていれば学年が上がっても計算力を順調に積み上げていけるのではないでしょうか。

（４年生）①２桁×１桁が暗算で答えらえる。
　　　　　②3桁÷2桁　3桁÷1桁が暗算で答えられる。
　　　　　③3.14の計算の暗算
　　　　　④11×11、12×12、13×13、・・・、19×19の暗算

＊①②２桁×１桁の計算は、暗算で答えなければいけないという環境があるか無いかが重要です。この時期、計算力がある、無いの個人差はあるでしょうが暗算で答えを出してみようと試みて暗算で答えられないまま５年生になった生徒はほとんどいなかったような気がします。
　③２×3.14、３×3.14、４×3.14、・・・９×3.14および１２×3.14の答えは
　　生徒に暗記してもらっています。
　　余力があれば、２×２×3.14、３×３×3.14、・・・９×９×3.14　まで。
　④図形（正方形の1辺の長さ）や規則性の問題で必要になります。

この4点がクリアできていれば学年が上がっても計算力を順調に積み上げていけるのではないでしょうか。
5年生になると単元の内容が難しくなってきます。これらの計算力が備わっていると授業を受けているときの生徒の負担もかなり軽減されるのではないでしょうか。

（５年生）①よく見かける数の2桁どうしの最小公倍数が暗算できる。
　　　　　②小数→分数、分数→小数　への相互の変換
　　　　　 ③テストの時など、計算用紙がしっかり作れる。
　　　　 ④その他計算の工夫

＊①計算問題では通分することが必要になります。文章題などでも最小公倍数を時間をかけずに算出しなければならないケースが多々出現してきます。
　②計算問題や文章題で必要になります。換算方法を知っている場合、計算がかなり楽になることが多いでしょう。
　③テストで計算問題を安定して得点するためには、計算用紙をしっかり作れることが必要になります。テストで計算を間違えたとき、もう一度解き直せば正解することができるでしょう。しかし、それでは計算ミスは減りません。テストが終わってから、自分で書いた計算用紙がしっかり残っていて、計算過程のどこでミスが出たのかを確認することが重要です。

（６年生）①計算ミスをしない
　　　　　②工夫して計算する

＊①入試はもちろんのこと、どんな模擬試験でも計算は間違えないことが前提。
　　計算を間違えたら、必ず自分で書いた計算用紙を振り返りどの部分で間違えたのかを必ずチェックしてください。
　②入試は時間を短縮して解ける問題は正解をだし、できるだけ応用的な問題に対して考える時間を確保することが戦略として必要になります。普段から意識して取り組んでください。

必ず復習をする

算数は復習なくして知識の定着は図れません。まず、授業で習った考え方をまねするとこ
ろから始まり、自分なりのアレンジが加わり実力がついていきます。復習は解いた問題全てを解き直すということではありません。宿題を行ったときにわからなかった問題で授業で解説してもらった問題や授業ではじめて習ったが考え方の理解が不十分な問題などを再び考え解いてみることを指します。そして、復習せずに寝てしまうとせっかく頭にはいっていたことの忘却速度が大きくなるのです。受験生の体力も必要ですし、、慣れるまでは大変だと思いますが、『習った当日中に復習する』ように近づけていってください。復習を行うから『わかっていない』ことがわかり、質問が生じるのです。そうやって発生した質問はやはり身につく度合いも大きいのです。
復習するタイミングがわからないとか、復習する時間がないとお悩みの声をよく耳にします。
そんなときは、ぜひ、ご相談ください。必ず1週間の中で復習する時間を組み込めるスケジュールを見つけることができると思います。一緒に考えていきましょう。

図・表・状況図などを書く

算数を苦手だと思っているみなさん。いつも問題を解いているとき、ノートに状況図をしっかり書いていますか。いきなり式を作って計算しようとしていませんか。
「だってかけないんだもん。」「書こうとは思っているんだけど・・」算数に苦手意識をお持ちの生徒さんからよく聞く言葉です。
そうです。生徒さんたちは書けるものなら状況図をしっかり書いて正解までたどり着きたいと誰もが思っているのです。
書けない原因は、①基本原理が定着していないこと　②書けるようになるまで練習が不足している　ことです。ことばで言うのは簡単ですが、これを生徒さん自身が自ずと実践できるようになるには「コツ」や「きっかけ」が必要です。

でもみなさん、不安にならないでください。「コツ」や「きっかけ」をみなさんと一緒に全力で見つけていこうと思います。とことんおつきあいします。
算数は本来、すごく楽しいものなのです。わからなかった問題が解けた時の喜び、解ける問題が多くなっていく喜び、そして算数が得意科目に変わっていく喜びをぜひみなさんと一緒に味わいましょう。みなさんにお会いできるのを楽しみにしております。

問題

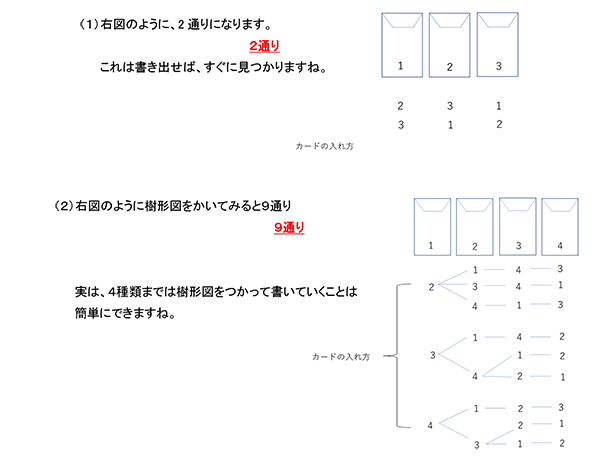
図のように、１から５までの数字がそれぞれひとつだけ書かれた封筒（ふうとう）とカードがあります。これらのカードを封筒の中に一枚ずつ入れるとき、次の問いに答えなさい。

• （１）１から３までの封筒と１から３までのカードを使うとき、封筒の数字とカードの数字が一組も同じにならないような入れ方は何通りありますか。
• （２）１から４までの封筒と１から４までのカードを使うとき、封筒の数字とカードの数字が一組も同じにならないような入れ方は何通りありますか。
• （３）１から５までの封筒と１から５までのカードを使うとき、封筒の数字とカードの数字が一組も同じにならないような入れ方は何通りありますか。

解答例

（３）もし、１の封筒に１のカードを入れた場合、２から５の封筒に２から５のカードを番号が一組も同じにならないような入れ方は、（２）と同じく4種類の封筒に4種類のカードを番号が一組も同じにならないような入れ方と同じになるので、９通りである。
２の封筒に２のカードを入れた場合も、残りの１，３，４，５のカードが１，３，４，５の封筒に番号が一組も同じにならないようになる入れ方は９通りになります。 ３の封筒に３のカードを入れた場合も、４の封筒に４のカードを入れた場合も、５の封筒に５のカードを入れた場合も、それぞれ９通りあります。
よって、9×5＝45通り

４５通り

入試問題の多くは、この（３）まで出題されることが多いのですが、もし、封筒とカードの数がもっと多い数で出題された場合、どのように対処すればよいでしょうか。
樹形図をかくことは重要なことです。しかし、あまりにも多いとかき続けることは困難ですよね。
ましてや、限られた試験時間のなかで書き漏れやミスすることができない状況ではなおさらです。
こんな問題だったらどうでしょう。
一緒に考えてみましょう。

問題

１から５までの番号が書かれた箱と１から５までの番号が書かれたボールがあります。
箱のなかにボールを１つずつ入れていきます。箱の番号とボールの番号が一組も同じにならない入れ方は何通りですか。

考え方を見ていきましょう。
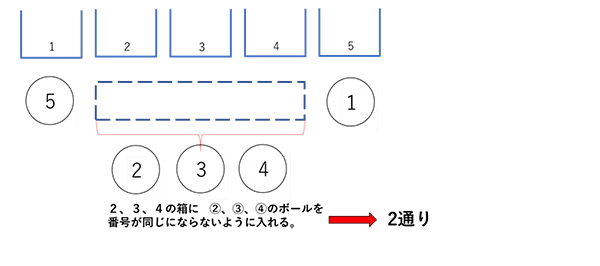
まず、１の箱に⑤が入る場合を調べてみます。
２、３、４、５の箱に①、②、③、④のボールを入れていくのですが、
このとき５の箱と①に注目すると、５の箱に①が入る場合と入らない場合（絶対にどちらかしかありませんよね。）があります。
下の図のように、５の箱に①が入る場合、２、３、４の箱に②、③、④のボールを番号が一組も同じにならない入れ方は、先ほどの問題の（１）と同じく2通りあります。
なぜなら、３種類の封筒に３種類のカードを入れることと同じだからです。

今度は、５の箱に①が入らない場合を考えてみます。

そこで少し考え方を工夫してみます。どうすれば２、３、４、５の箱に①、②、③、④のボールを番号が同じにならないように、しかも５の箱に①が入らない入れ方を考えていけばよいのでしょうか。
ここが重要なポイントです。
今だけ、①を⑤のつもりで考えるのです。
もし、①を⑤だと思えば、⑤は５の箱に入れないわけですから、当然①は５の箱には入れないわけです。

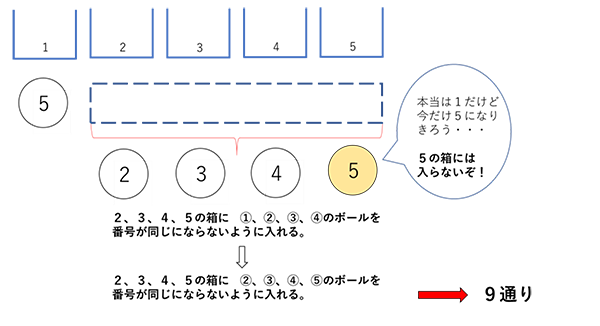
よって、１の箱に⑤が入る場合、2＋9＝11通り　です。
１の箱に②、③、④が入る場合もそれぞれ１１通りずつあります。
したがって、（2＋9）×4＝44通り　ということになります。
では、さらに６種類の箱とボールで同じ番号どうしにならないような入れ方を考えてみます。
５個の箱と５個のボールの時と考え方は同じです。

下の図のように、１の箱に⑥が入る場合を考えます。
さらに、６の箱に①は入る場合と入らない場合しかないので、
まず、６の箱に①が入る場合、２、３、４、５の箱に②、③、④、⑤のボールを一組も同じ番号にならないようする入れ方は、４種類の箱に４種類のボールを同じ番号にならないようにする入れ方とおなじになりますから、９通りになります。

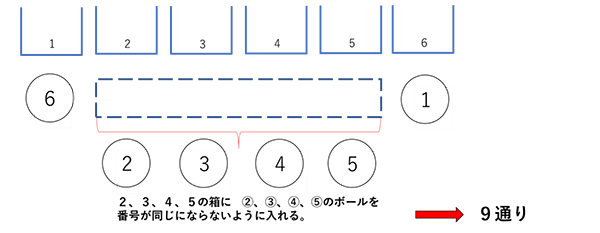
今度は、６の箱に①が入らない場合を考えてみます。
どう考えればよかったんでしたっけ？
そうです。①を⑥のつもりで考えれば良かったんです。
もし、①を⑥だと思えば、⑥は６の箱に入れないわけですから、当然①は６の箱には入れないわけです。

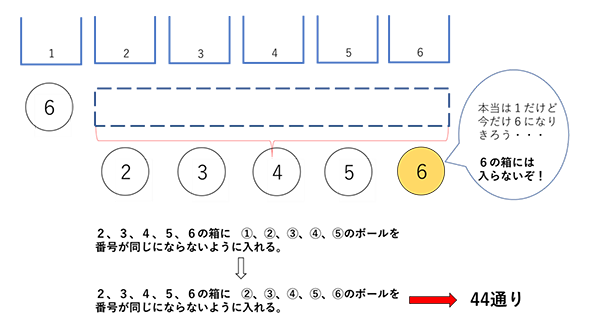
よって、１の箱に⑥が入る場合、9＋44＝53通り　です。
１の箱に②、③、④、⑤が入る場合もそれぞれ53通りずつあります。
したがって、（9＋44）×5＝265通り　ということになります。
実は、こんなしくみになっています。