第1章　濃度の「偏差値２０アップ・指導法」例題① ｜中学受験の勉強法　偏差値20アップの学習法

第1章　濃度の「偏差値２０アップ・指導法」例題①

１．２　例題（例題で根本原理を確認）

１．１の導入で学習した根本原則（①面積図、②逆比、③体系）が実際の問題でどのように問われているのかを、
１．１の【ケース１】～【ケース２】の典型例題で確認することが偏差値２０アップノウハウでは重要です。

例題１

【ケース１の例題】《　面積図の式で解けるケース　》
濃さが１２％の食塩水が１５０gあります。この食塩水に食塩を加えて、濃さが２０％の食塩水にするには、何gの食塩を加えるとよいですか。

【ポイント】

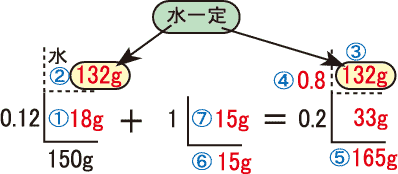
水が一定であることを利用①〜⑦の順に解けばよい。
①　0.12×150=18g … はじめの食塩
②③　150-18=132g … はじめの水のまま
④　1-0.2=0.8 … 最終的な水の割合
⑤　132÷0.8=165g … 最終的な全体量
⑥⑦　165-150=15g … 加えた食塩

従来の塾の解説方法によると、「水が一定」を暗記させていたが、左のように水の面積図を乗せると、水が一定だということが目で見て分かる。このイメージづけが「20アップ指導法」です。

例題２

【ケース２の例題】《　面積図の流れ図で解けるケース　》
容器Aには２０％の食塩水１００gが、容器Bには２％の食塩水１００gが入っています。今、容器AからBへ２０g移し、次にBからAへ２０g移すとAの食塩水は何％になりますか。

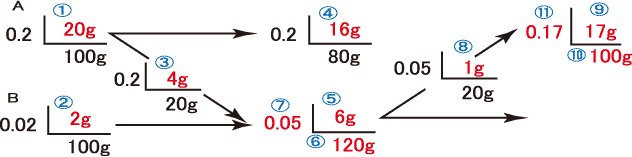
① 100×0.2=20g … はじめのAの食塩	⑦ 6÷120=0.05 … 新しいBの濃度
② 100×0.02=2g … はじめのBの食塩	⑧ 20×0.05=1g … BからAへの食塩
③ 20×0.2=4g … AからBへの食塩	⑨ 16+1=17g … 新しいAの食塩
④ 20-4=16g … Aに残った食塩	⑨ 16+1=17g … 新しいAの食塩
⑤ 4+2=6g … 新しいBの中の食塩	⑩ 80+20=100g … 新しいAの食塩
⑥ 100+20=120g … 新しいBの食塩水	⑪ 17÷100=0.17 … 新しいAの濃度

ケース１のように面積図の式では描けないことを意識させる。
また、勉強勉強せず、パズルのようにゲーム性を持たせて、楽しませることが重要。中学受験の算数を数学のように学問とはとらえず、「工夫する遊び」あるいは「文系科目」と捉え、塾で教わった解き方でも良いし、この解き方でもよく、工夫することの楽しさを指導すべきです。この考え方が小学生に受け入れられやすく、ひいては「20アップ指導法」となる。

例題３

【ケース３の例題】《　平均算の面積図で解けるケース　》
７％の食塩水Agと、１２％の食塩水Bgを混ぜると、９％の食塩水が３００gできます。　７％と１２％の食塩水は、それぞれ何gずつ混ぜましたか。

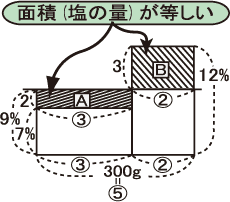
① 右の図で、長方形Bの塩が長方形Aに移るから、
AとBの塩の量は等しい（面積が等しい）。
③ 面積が等しい場合→横の比とたての比は逆比となるから
④ 長方形AとBにおいて、
(たての比)=(9%-7%)：(12%-9%)=2：3より、
(横の比)=③：②と逆比になる。
このため、300g=⑤と分かる。
⑤ 300÷⑤=60gより、60g=1となるから、
⑥ A=60×③=180g　　B=60×②=120g

【別解】(てんびん図を利用)

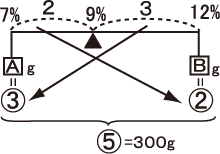
(てんびんの腕の長さの比)=(9-7)：(12-9)=2：3より
(AとBの重さの比は)=③：②の逆比になる。
したがって、300÷60g … ①(あとは上の解答と同じ)

①「A％とB％を混ぜるとC％になる」という問題で、食塩水の量が一箇所（300g）しか分かっていない問題の場合、【ケース１、２】では解けません。そこで、右図のように、平均算のように、面積図を横にくっつけた図を書いて、「平均算」を利用して解きます。
②「てんびん図」の解法は、最近若い先生の間ではやっているが、割合を表現できないので、応用に弱い。しかし、パターンにはまれば短時間で解けるので、テスト用に覚えておくと良いでょう。

« 第1章　濃度の「偏差値２０アップ・指導法」導入②逆比

第1章　濃度の「偏差値２０アップ・指導法」例題② »